题目内容
16.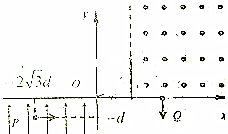 如图所示,在平面直角坐标系xOy中的第Ⅲ象限内充满+y方向的匀强电场,第Ⅰ象限的虚线右侧区域内有垂直与纸面向外的匀强磁场,一个质量为m、带电量为q的带电粒子以大小为v0的初速度自P点(-2$\sqrt{3}d$,-d)沿+x方向运动.恰经原点O进入第Ⅰ象限,粒子穿过匀强磁场后,最终垂直通过x轴上的点Q进入第Ⅳ象限,已知匀强磁场的磁感应强度B=$\frac{m{v}_{0}}{qd}$.不计粒子重力.求:
如图所示,在平面直角坐标系xOy中的第Ⅲ象限内充满+y方向的匀强电场,第Ⅰ象限的虚线右侧区域内有垂直与纸面向外的匀强磁场,一个质量为m、带电量为q的带电粒子以大小为v0的初速度自P点(-2$\sqrt{3}d$,-d)沿+x方向运动.恰经原点O进入第Ⅰ象限,粒子穿过匀强磁场后,最终垂直通过x轴上的点Q进入第Ⅳ象限,已知匀强磁场的磁感应强度B=$\frac{m{v}_{0}}{qd}$.不计粒子重力.求:(1)求第Ⅲ象限内匀强电场的场强E的大小;
(2)Q点的坐标xQ.
分析 (1)粒子在第Ⅲ象限做类平抛运动,根据类似平抛运动的分位移公式和牛顿第二定律列式求解即可;
(2)先根据类平抛运动的分运动公式求解末速度,然后根据磁场中洛伦兹力等于向心力列得求解轨道半径,再结合几何关系得到Q点的坐标xQ.
解答 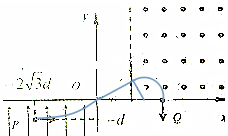 解:(1)粒子在第Ⅲ象限做类平抛运动,则有:
解:(1)粒子在第Ⅲ象限做类平抛运动,则有:
2$\sqrt{3}$d=v0t …①
d=$\frac{1}{2}$at2 …②
又由牛顿第二定律得:a=$\frac{qE}{m}$…③
解得:E=$\frac{m{v}_{0}^{2}}{6qd}$…④
(2)设粒子到达O点瞬间,速度大小为v,与x轴夹角为α:
则有:d=$\frac{{v}_{y}}{2}t$ …⑤
由①⑤解得:vy=$\frac{\sqrt{3}}{3}{v}_{0}$…⑥
tanα=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{\sqrt{3}}{3}$,α=$\frac{π}{6}$…⑦
粒子在磁场中,洛伦兹力提供向心力:
qvB=$\frac{m{v}^{2}}{R}$…⑧
解得,粒子在匀强磁场中运动的半径:R=$\frac{mv}{qB}$=$\frac{m•\frac{\sqrt{3}}{3}{v}_{0}}{q•\frac{m{v}_{0}}{qd}}$=$\frac{\sqrt{3}}{3}$d…⑨
根据几何知识得:Q点的坐标为:xQ=R+$\frac{R}{sin30°}$=3R=$\sqrt{3}$d
答:(1)第Ⅲ象限内匀强电场的场强E的大小为$\frac{m{v}_{0}^{2}}{6qd}$;
(2)Q点的坐标xQ为$\sqrt{3}$d.
点评 本题关键是明确粒子的运动规律,对于类平抛运动过程,根据分运动公式列式分析,对于圆周运动过程,根据牛顿第二定律列式分析,同时要画出轨迹分析.

 如图所示,竖直平面内的轨道Ⅰ和轨道Ⅱ都由两段细直杆连接而成,两轨道长度相等.用相同的水平恒力将穿在轨道最低点B的静止小球分别沿Ⅰ和Ⅱ拉至最高点A,所需时间分别为t1、t2,动能增量分别为△Ek1、△Ek2.假定球在经过轨道转折点前后速度的大小不变,若球与Ⅰ、Ⅱ轨道间接触面光滑,则( )
如图所示,竖直平面内的轨道Ⅰ和轨道Ⅱ都由两段细直杆连接而成,两轨道长度相等.用相同的水平恒力将穿在轨道最低点B的静止小球分别沿Ⅰ和Ⅱ拉至最高点A,所需时间分别为t1、t2,动能增量分别为△Ek1、△Ek2.假定球在经过轨道转折点前后速度的大小不变,若球与Ⅰ、Ⅱ轨道间接触面光滑,则( )| A. | △Ek1>△Ek2 | B. | △Ek1=△Ek2 | C. | t1>t2 | D. | t1<t2 |
| 行星名称 | 水星 | 金星 | 地球 | 火星 | 木星 | 土星 | 天王星 | 海王星 |
| 星球半径 (×106 m) | 2.44 | 6.05 | 6.37 | 3.39 | 69.8 | 58.2 | 23.7 | 22.4 |
| 轨道半径 (×1011 m) | 0.579 | 1.08 | 1.50 | 2.28 | 7.78 | 14.3 | 28.7 | 45.0 |
| A. | 10年 | B. | 30年 | C. | 50年 | D. | 100年 |
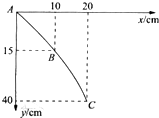 如图是小球做平抛运动的一段运动轨迹,A、B、C为运动轨迹上的三点,以A为坐标原点,建立坐标系,各点坐标值已在图中标出点在轨迹上,取重力加速度g=10m/s2,则小球做平抛运动的初速度为( )
如图是小球做平抛运动的一段运动轨迹,A、B、C为运动轨迹上的三点,以A为坐标原点,建立坐标系,各点坐标值已在图中标出点在轨迹上,取重力加速度g=10m/s2,则小球做平抛运动的初速度为( )| A. | 0.5m/s | B. | 1m/s | C. | 1.5m/s | D. | 2m/s |
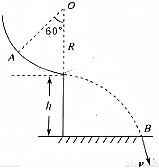 如图所示,小球在光滑的圆弧上由A点静止释放,离开圆弧之后在空中运动落到地上的B点,已知O点为圆弧的圆心,圆弧底端离地面高度为h.小球到达地面时速度的大小是$\sqrt{g(R+2h)}$.
如图所示,小球在光滑的圆弧上由A点静止释放,离开圆弧之后在空中运动落到地上的B点,已知O点为圆弧的圆心,圆弧底端离地面高度为h.小球到达地面时速度的大小是$\sqrt{g(R+2h)}$.