题目内容
7. 如图所示,竖直平面内的轨道Ⅰ和轨道Ⅱ都由两段细直杆连接而成,两轨道长度相等.用相同的水平恒力将穿在轨道最低点B的静止小球分别沿Ⅰ和Ⅱ拉至最高点A,所需时间分别为t1、t2,动能增量分别为△Ek1、△Ek2.假定球在经过轨道转折点前后速度的大小不变,若球与Ⅰ、Ⅱ轨道间接触面光滑,则( )
如图所示,竖直平面内的轨道Ⅰ和轨道Ⅱ都由两段细直杆连接而成,两轨道长度相等.用相同的水平恒力将穿在轨道最低点B的静止小球分别沿Ⅰ和Ⅱ拉至最高点A,所需时间分别为t1、t2,动能增量分别为△Ek1、△Ek2.假定球在经过轨道转折点前后速度的大小不变,若球与Ⅰ、Ⅱ轨道间接触面光滑,则( )| A. | △Ek1>△Ek2 | B. | △Ek1=△Ek2 | C. | t1>t2 | D. | t1<t2 |
分析 根据动能定理比较动能的增加量;通过速度时间图线,抓住路程相等,结合加速度不同,比较运动时间的长短.
解答 解:A、B、因为摩擦力做功Wf=μ(mgcosθ+Fsinθ)•s=μmgx+μFh,可知沿两轨道运动,摩擦力做功相等,根据动能定理得:
WF-mgh-Wf=△Ek,
知两次情况拉力做功相等,摩擦力做功相等,重力做功相等,则动能的变化量相等.故A错误,B正确;
C、D、设物体的加速度a,则:ma=Fcosθ-mgsinθ-μ(mgcosθ+Fsinθ)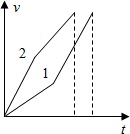
可知斜面与水平面之间的夹角越大,加速度越小,结合物体运动的轨迹,作出在两个轨道上运动的速度时间图线如图所示,由于路程相等,则图线与时间轴围成的面积相等,由图可知,t1>t2.故C正确,D错误.
故选:BC.
点评 本题考查了动能定理与运动学的综合,通过动能定理比较动能变化量的关系,难点在于通过速度时间图线比较运动的时间,知道图线的斜率表示加速度,图线与时间轴围成的面积表示位移.

练习册系列答案
相关题目
17. 如图,人到靶盘的距离为d,沿水平方向掷出的飞镖初速度为V0,抛射点高于靶心的高度,结果飞镖射在靶心正下方h处,为了使靶准确的射中靶心,下列方法不可行的是( )
如图,人到靶盘的距离为d,沿水平方向掷出的飞镖初速度为V0,抛射点高于靶心的高度,结果飞镖射在靶心正下方h处,为了使靶准确的射中靶心,下列方法不可行的是( )
 如图,人到靶盘的距离为d,沿水平方向掷出的飞镖初速度为V0,抛射点高于靶心的高度,结果飞镖射在靶心正下方h处,为了使靶准确的射中靶心,下列方法不可行的是( )
如图,人到靶盘的距离为d,沿水平方向掷出的飞镖初速度为V0,抛射点高于靶心的高度,结果飞镖射在靶心正下方h处,为了使靶准确的射中靶心,下列方法不可行的是( )| A. | 只增大飞镖的初速度V0,其它条件不变 | |
| B. | 只增大抛射点的高度,其它条件不变 | |
| C. | 只减小人到靶盘的距离为d,其它条件不变 | |
| D. | 只减小飞镖的重量,其它条件不变 |
18.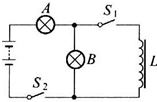 如图所示,A、B是两盏完全相同的白炽灯,L是直流电阻不计、自感系数很大的自感线圈,如果断开电键S1,闭合S2,A、B两灯都能同样发光.如果最初S1是闭合的,S2是断开的.那么不可能出现的情况是( )
如图所示,A、B是两盏完全相同的白炽灯,L是直流电阻不计、自感系数很大的自感线圈,如果断开电键S1,闭合S2,A、B两灯都能同样发光.如果最初S1是闭合的,S2是断开的.那么不可能出现的情况是( )
 如图所示,A、B是两盏完全相同的白炽灯,L是直流电阻不计、自感系数很大的自感线圈,如果断开电键S1,闭合S2,A、B两灯都能同样发光.如果最初S1是闭合的,S2是断开的.那么不可能出现的情况是( )
如图所示,A、B是两盏完全相同的白炽灯,L是直流电阻不计、自感系数很大的自感线圈,如果断开电键S1,闭合S2,A、B两灯都能同样发光.如果最初S1是闭合的,S2是断开的.那么不可能出现的情况是( )| A. | 刚一闭合S2,A灯就亮,而B灯则延迟一段时间才亮 | |
| B. | 刚闭合S2时,线圈L中的电流为零 | |
| C. | 闭合S2以后,A灯变亮,B灯由亮变暗 | |
| D. | 再断开S2时,A灯立即熄火,B灯先亮一下然后熄灭 |
15.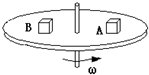 如图所示,A、B两物块置于竖直轴匀速转动的水平圆盘上,A物块距轴较近,两物块始终相对圆盘静止,下列关于两物块的说法,错误的是( )
如图所示,A、B两物块置于竖直轴匀速转动的水平圆盘上,A物块距轴较近,两物块始终相对圆盘静止,下列关于两物块的说法,错误的是( )
 如图所示,A、B两物块置于竖直轴匀速转动的水平圆盘上,A物块距轴较近,两物块始终相对圆盘静止,下列关于两物块的说法,错误的是( )
如图所示,A、B两物块置于竖直轴匀速转动的水平圆盘上,A物块距轴较近,两物块始终相对圆盘静止,下列关于两物块的说法,错误的是( )| A. | 线速度相同 | B. | 周期相同 | C. | 角速度相同 | D. | 转速相同 |
2.可发射一颗人造卫星,下列哪种轨道不能实现( )
| A. | 与地球表面上某一纬度线(非赤道)是共面的同心圆 | |
| B. | 与地球表面上的赤道线是共面椭圆,且地球处于椭圆轨道的一个焦点上 | |
| C. | 与地球表面上的赤道线是共面同心圆,且卫星相对地面是运动的 | |
| D. | 与地球表面上的赤道线是共面同心圆,且卫星相对地面是静止的 |
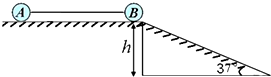 如图所示,光滑水平面与倾角为θ=37°光滑斜面平滑连接,斜面高度为h=5m,质量为mA=3kg的物体A与质量为mB=1kg的物体B通过长为2.5h轻绳连接,开始时,轻绳刚好绷直,物体B位于水平面边缘,由于受到轻微扰动,物体B由静止开始沿斜面下滑,当滑到斜面底端时,由于某种原因轻绳与AB脱离.物体A和B均可看成质点,g取10m/s2.求:(取sin37°=0.6,cos37°=0.8;AB可视为质点.)
如图所示,光滑水平面与倾角为θ=37°光滑斜面平滑连接,斜面高度为h=5m,质量为mA=3kg的物体A与质量为mB=1kg的物体B通过长为2.5h轻绳连接,开始时,轻绳刚好绷直,物体B位于水平面边缘,由于受到轻微扰动,物体B由静止开始沿斜面下滑,当滑到斜面底端时,由于某种原因轻绳与AB脱离.物体A和B均可看成质点,g取10m/s2.求:(取sin37°=0.6,cos37°=0.8;AB可视为质点.)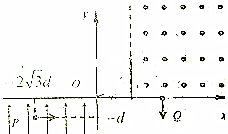 如图所示,在平面直角坐标系xOy中的第Ⅲ象限内充满+y方向的匀强电场,第Ⅰ象限的虚线右侧区域内有垂直与纸面向外的匀强磁场,一个质量为m、带电量为q的带电粒子以大小为v0的初速度自P点(-2$\sqrt{3}d$,-d)沿+x方向运动.恰经原点O进入第Ⅰ象限,粒子穿过匀强磁场后,最终垂直通过x轴上的点Q进入第Ⅳ象限,已知匀强磁场的磁感应强度B=$\frac{m{v}_{0}}{qd}$.不计粒子重力.求:
如图所示,在平面直角坐标系xOy中的第Ⅲ象限内充满+y方向的匀强电场,第Ⅰ象限的虚线右侧区域内有垂直与纸面向外的匀强磁场,一个质量为m、带电量为q的带电粒子以大小为v0的初速度自P点(-2$\sqrt{3}d$,-d)沿+x方向运动.恰经原点O进入第Ⅰ象限,粒子穿过匀强磁场后,最终垂直通过x轴上的点Q进入第Ⅳ象限,已知匀强磁场的磁感应强度B=$\frac{m{v}_{0}}{qd}$.不计粒子重力.求: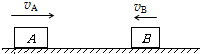 如图所示,光滑水平面上有A、B两物块,已知A物块的质量为2kg,以4m/s的速度向右运动,B物块的质量为1kg,以2m/s的速度向左运动,两物块碰撞后粘在一起共同运动.若规定向右为正方向,则碰撞前B物块的动量为-2kg•m/s,碰撞后共同速度为2m/s.
如图所示,光滑水平面上有A、B两物块,已知A物块的质量为2kg,以4m/s的速度向右运动,B物块的质量为1kg,以2m/s的速度向左运动,两物块碰撞后粘在一起共同运动.若规定向右为正方向,则碰撞前B物块的动量为-2kg•m/s,碰撞后共同速度为2m/s.