��Ŀ����
����Ŀ����ͼ��ʾ����ֱƽ���ڷ�һֱ�Ǹˣ��˵�ˮƽ���ֲִڣ��˵���ֱ���ֹ⻬�������ָ�����������Ϊ1kg��С��A��B��A��B����ϸ��������A��ˮƽ��֮��Ķ�Ħ������![]() =0.2����ʼA��B�����ھ�ֹ״̬����֪��OA=3m��OB=4m����A����ˮƽ����F�����������һ������ƶ�1m(ȡg=10m/s2)����ô�ù�����( )
=0.2����ʼA��B�����ھ�ֹ״̬����֪��OA=3m��OB=4m����A����ˮƽ����F�����������һ������ƶ�1m(ȡg=10m/s2)����ô�ù�����( )
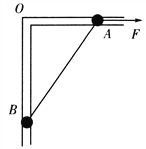
A. С��A�ܵ���Ħ������СΪ7.5N
B. С��B�����ľ���Ϊ1m
C. ����F����Ϊ12J
D. ����F����Ϊ14J
���𰸡�BD
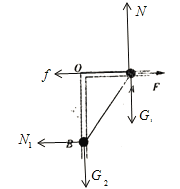
�������������������AB��������������������F������G��֧����N�������Ħ����f�����ҵĵ���N1�����ݹ�����ƽ��������ʽ�����֧����N���Ӷ��õ�����Ħ���������ݼ���֪ʶ���B�������ĸ߶ȣ������������ö��ܶ�����ʽ���õ������Ĺ���
��AB��������������������F������G��֧����N�������Ħ����f�����ҵĵ���![]() ����ͼ�����ݹ�����ƽ������������ֱ����
����ͼ�����ݹ�����ƽ������������ֱ���� ![]() ��ˮƽ����
��ˮƽ���� ![]() ������
������![]() �����
�����![]() ��
�� ![]() ��A�����ƶ�ǰ������
��A�����ƶ�ǰ������![]() ��A���ƶ�1m��OA=4m����OB��Ϊ
��A���ƶ�1m��OA=4m����OB��Ϊ![]() ������С��B����1m��B��ȷ���������������˶����������ö��ܶ�����ʽ���õ�
������С��B����1m��B��ȷ���������������˶����������ö��ܶ�����ʽ���õ�![]() ������
������![]() ��C����D��ȷ��
��C����D��ȷ��

 ��ǰ����ϵ�д�
��ǰ����ϵ�д�