题目内容
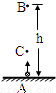
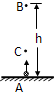 从地面A处竖直上抛一质量为m的小球,当小球上升到距A点高度为h的B点时动能为EK;当小球上升到最高点后返回至距A处h/3的C点时,动能也为EK.已知空气阻力f=0.1mg,则小球能上升的最大高度为
从地面A处竖直上抛一质量为m的小球,当小球上升到距A点高度为h的B点时动能为EK;当小球上升到最高点后返回至距A处h/3的C点时,动能也为EK.已知空气阻力f=0.1mg,则小球能上升的最大高度为4
4
h;小球在下落过程中从B点到C点克服空气阻力所做的功为| 1 |
| 15 |
| 1 |
| 15 |
分析:对小球从A点运动到B点和返回C点的两个过程运用动能定理列式,即可求解最大高度,从上升到的B点运动到下落时的B点的过程中运用动能定理结合小球上升到B点时的动能与小球上升到最高点后返回至C点时的动能相等可求得小球下落过程中从B点到C点动能的增量.
解答:解:设最大高度为H,则
对小球,从A点运动到B点的过程,由动能定理得:EK-
m
=-(mg+f)h
从A点开始运动到返回C点的过程运用动能定理得:EK-
m
=-mg?
h-f(2H-
h)
又f=0.1mg
联立解得:H=4h
从上升到B点运动到下落时B点的过程中运用动能定理得:
EK′-EK=-f(3h+3h),
在下落过程中从B点到C点,有 mg(h-
h)-W=EK-EK′
联立以上两式得:W=
mgh
故答案为:4,
对小球,从A点运动到B点的过程,由动能定理得:EK-
| 1 |
| 2 |
| v | 2 A |
从A点开始运动到返回C点的过程运用动能定理得:EK-
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 3 |
| 1 |
| 3 |
又f=0.1mg
联立解得:H=4h
从上升到B点运动到下落时B点的过程中运用动能定理得:
EK′-EK=-f(3h+3h),
在下落过程中从B点到C点,有 mg(h-
| 1 |
| 3 |
联立以上两式得:W=
| 1 |
| 15 |
故答案为:4,
| 1 |
| 15 |
点评:本题是动能定理的应用,要选择合适的过程进行列式研究,难度适中.

练习册系列答案
相关题目
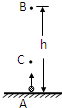 从地面A处竖直上抛一质量为m的小球,小球上升到B点时的动能与小球上升到最高点后返回至C点时的动能相等,B点离地高度为h,C点离地高度为
从地面A处竖直上抛一质量为m的小球,小球上升到B点时的动能与小球上升到最高点后返回至C点时的动能相等,B点离地高度为h,C点离地高度为| h |
| 3 |
| A、小球上升的最大高度为3h |
| B、小球从抛出到落地过程动能减少0.8mgh |
| C、小球从上升经过B点到下落经过B点过程动能的增量为0 |
| D、小球下落过程中从B点到C点动能的增量为0.6mgh |
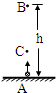 (2013?长宁区一模)从地面A处竖直上抛一质量为m的小球,小球上升到B点时的动能与小球上升到最高点后返回至C点时的动能相等,B点离地高度为h,C点离地高度为
(2013?长宁区一模)从地面A处竖直上抛一质量为m的小球,小球上升到B点时的动能与小球上升到最高点后返回至C点时的动能相等,B点离地高度为h,C点离地高度为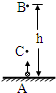
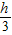 .空气阻力f=0.1mg,大小不变,则小球上升的最大高度为______;小球下落过程中从B点到C点动能的增量为______.
.空气阻力f=0.1mg,大小不变,则小球上升的最大高度为______;小球下落过程中从B点到C点动能的增量为______.