题目内容
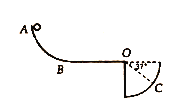
【题目】如图所示，水平桌面由粗糙程度不同的AB、BC两部分组成，且AB= 
BC，小物块P（可视为质点）以某一初速度从A点滑上桌面，最后恰好停在C点，已知物块经过AB与BC两部分的时间之比为1：4，则物块P与桌面上AB、BC部分之间的动摩擦因数μ1、μ2之比为（P物块在AB、BC上所做的运动均可看作匀变速直线运动）（ ）
A.1：4
B.4：1
C.8：1
D.16：1
【答案】D
【解析】解：设B点的速度为vB，根据AB= 
BC及匀变速直线运动平均速度的推论有：
t1= × 
t2，
又t1：t2=1：4
在AB上的加速度大小为：a1=μ1g= 
BC上的加速度大小为：a2=μ2g= 
联立解得：μ1：μ2=16：1．
故D正确，ABC错误．
故选：D
【考点精析】通过灵活运用匀变速直线运动的速度、位移、时间的关系，掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值即可以解答此题．
练习册系列答案
相关题目
