Question

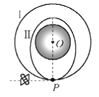
【题目】在竖直平面内，支在原点的一根弯杆，其形状可以用函数来描写，为有长度量纲的非零正常数，在杆上穿一滑块，杆与滑块间的静摩擦因数为，如图所示。

(1)不考虑摩擦，求滑块的高度为时，它在沿杆方向的加速度的大小，下列5种答案中有一个是正确的，试作出判断并说明理由：，，，，；

(2)考虑摩擦，但杆不动，在什么情况下滑块可以在杆上静止？（用，，，表示）

(3)现在设杆以角速度绕轴匀速转动，且有关系，这时滑块可以在何处相对于杆静止？

(4)若，则滑块不滑动的条件又如何？

Answer 1

【答案】(1)；(2)；(3)；(4)或

【解析】

(1)由分析知道在不考虑摩擦时，滑块在杆上运动的加速度即为重力加速度的切向分量

其中为滑块所在点杆的法线与重力方向的夹角，一般不为零，且一定不超过，当时，杆近于竖直，趋近于，于是可判断

由此可得

，

(2)由分析知道考虑摩擦而杆不动，则滑块静止为静力平衡，滑块受重力影响有下滑趋势，摩擦力向上，支持力和摩擦力大小分别为

，

平衡条件要求

或

设时，则滑块静止的条件为

(3)由分析知道当杆匀速转动时，则在滑块相对于杆不动时，支持力和摩擦力在竖直方向的分力之和与重力平衡，在水平方向的分力之和使滑块产生水平的向心加速度，由此可得（不妨设摩擦力沿杆向上）

由以上二式可得，

，

当时，有，即无摩擦力。

向心加速度完全由重力和支持力的合力提供，这个关系对任何都能满足，即此时滑块在任何位置都相对于杆静止。

(4)当时，，由

可知，即摩擦力实际是向下的，由于旋转太快而滑块上有上移的趋势，滑块相对静止的条件为

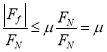
即

或

此二次函数不等式的判别式为

故不等式满足的条件为

或

用

代入，即得滑块不滑动的条件为

或