题目内容
【题目】如图所示，两根相距L=0.5 m的光滑平行金属导轨MN、PQ处于同一水平面内，导轨的左端用R=3 Ω的电阻相连，导轨电阻不计，导轨上跨接一电阻r=1 Ω的金属杆ab，质量m=0.2 kg，整个装置放在竖直向上的匀强磁场中，磁感应强度B=2 T，现对杆施加水平向右的拉力F=2 N，使它由静止开始运动，求：
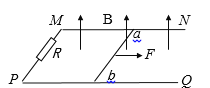
（1）杆能达到的最大速度vm为多大？
（2）若已知杆从静止开始运动至最大速度的过程中通过的位移x1=10 m，电阻R上产生的电热QR为多少？
（3）若杆达到最大速度后撤去拉力，则其继续向前运动的最大位移x2多大？
【答案】vm=8 m/s；QR= 10.2 J；x2=6.4 m
【解析】
（1）当导体棒加速度为零时，速度最大，根据平衡条件，有：F=F安=ILB，感应电流：I= 
代入数据联立可得vm=8 m/s
（2）对导体棒由动能定理可得： Fx1+W安= 
mv2，根据功能关系有：Q=－W安，因为外电阻与内阻为串联关系，根据焦耳定律可知：QR= 
Q ，联立可得QR= 10.2 J
（3）对导体棒由动量定理可得：－BLIt = 0－mv，感应电动势：
，电流：
，电量：
= 
，联立可得x2=6.4 m
【题目】在测定金属的电阻率的实验中，某种待测材料金属丝接入电路部分的长度约为50cm，所用测量仪器均已校准。
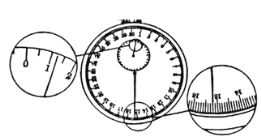
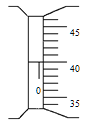
（1）用螺旋测微器测量金属丝的直径，其中某一次测量结果如图所示，其读数应为______mm（该值接近多次测量的平均值）。
（2）某实验小组用伏安法测金属丝的电阻Rx，记录实验数据如下表：
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
U／V | 0．10 | 0．30 | 0．70 | 1．00 | 1．50 | 1．70 | 2．30 |
I／A | 0．02 | 0．06 | 0．16 | 0．22 | 0．34 | 0．46 | 0．52 |
由以上实验数据可知：
①本实验的电流表选用的是____、电压表选用的是___、滑动变阻器选用的是____（填写以下器材前的字母）。
A．电流表A1（0～100 mA，内阻约为10 Ω）
B．电流表A2（0～0．6 A，内阻约为0．1 Ω）
C．电压表V1（0～3 V，内阻约为3 kΩ）
D．电压表V2（0～15 V，内阻约为15 kΩ）
E．滑动变阻器R1（0～1000 Ω，0．2 A）
F．滑动变阻器R2（0～20 Ω，2 A）
②测量Rx是采用下图中的____（填“甲”“乙”“丙”或“丁”）电路图。
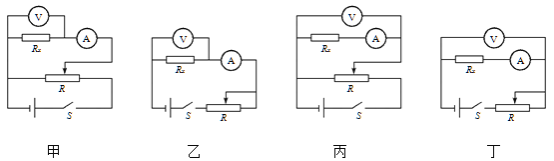
③可以估算出金属丝电阻率约为____（填选项前的字母）。
A．1×10－2Ω·m
B．1×10－3Ω·m
C．1×10－6Ω·m
D．1×10－8Ω·m
