题目内容
如图5-13所示,斜劈B的倾角为30°,劈尖顶着竖直墙壁静止于水平地面上,现将一个质量与斜劈质量相同、半径为r的球A放在墙面与斜劈之间,并从图示位置由静止释放,不计一切摩擦,求此后运动中
(1)斜劈的最大速度.
(2)球触地后弹起的最大高度。(球与地面作用中机械能的损失忽略不计)
(1)斜劈的最大速度.
(2)球触地后弹起的最大高度。(球与地面作用中机械能的损失忽略不计)

(1)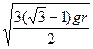 (2)
(2)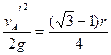
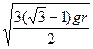 (2)
(2)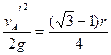
(1)A加速下落,B加速后退,当A落地时,B速度最大,整大过程中,斜面与球之间弹力对球和斜面做功代数和为零,所以系统机械能守恒.
mg(h-r)=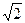 mvA2+
mvA2+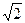 mvB2 ①
mvB2 ①
由图中几何知识知:h=cot30°·r=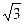 r ②
r ②
A、B的运动均可分解为沿斜面和垂直斜面的运动,如图5′—3所示。
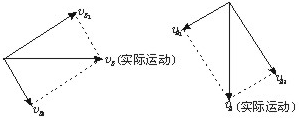
图5′—3
由于两物体在垂直斜面方向不发生相对运动,所以vA2=vB2
即vAcos30°=vBsin30° ③
解得vA=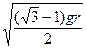
vB=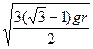
(2)A球落地后反弹速度vA′=vA
做竖直上抛运动的最大高度:Hm=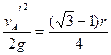
mg(h-r)=
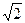 mvA2+
mvA2+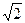 mvB2 ①
mvB2 ①由图中几何知识知:h=cot30°·r=
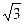 r ②
r ②A、B的运动均可分解为沿斜面和垂直斜面的运动,如图5′—3所示。

图5′—3
由于两物体在垂直斜面方向不发生相对运动,所以vA2=vB2
即vAcos30°=vBsin30° ③
解得vA=
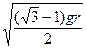
vB=
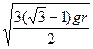
(2)A球落地后反弹速度vA′=vA
做竖直上抛运动的最大高度:Hm=
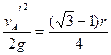

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目

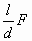 .由此说明,为什么越锋利的切削工具越容易劈开物体.
.由此说明,为什么越锋利的切削工具越容易劈开物体.
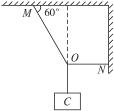
 向右运动,在A处环被挡住而停止的瞬间,绳子所受拉力为多少?在以后的运动过程中,球是先碰墙还是先碰地?第一次碰撞点离B点的距离是多少?(已知A处离墙的水平距离为L,球离地的高度h=2L).
向右运动,在A处环被挡住而停止的瞬间,绳子所受拉力为多少?在以后的运动过程中,球是先碰墙还是先碰地?第一次碰撞点离B点的距离是多少?(已知A处离墙的水平距离为L,球离地的高度h=2L).

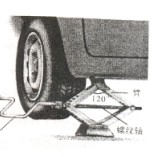
 N,此时千斤顶两臂间的夹角为120。,则下列判断正确的是
N,此时千斤顶两臂间的夹角为120。,则下列判断正确的是 N
N