Question

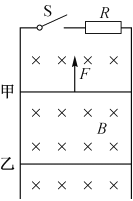
【题目】如图所示，足够长的“U”形框架沿竖直方向固定，在框架的顶端固定一定值电阻R，空间有范围足够大且垂直纸面向里的匀强磁场，磁感应强度大小为B，电阻值均为R的金属棒甲、乙垂直地放在框架上，已知两金属棒的质量分别为m=2.0×10-2kg、m乙=1.0×10-2kg。现将金属棒乙锁定在框架上，闭合电键，在金属棒甲上施加一竖直向上的恒力F，经过一段时间金属棒甲以v=10m/s的速度向上匀速运动，然后解除锁定，金属棒乙刚好处于静止状态，忽略一切摩擦和框架的电阻，重力加速度g=10m/s2。则

(1)恒力F的大小应为多大？

(2)保持电键闭合，将金属棒甲锁定，使金属棒乙由静止释放，则金属棒乙匀速时的速度v2应为多大？

(3)将两金属棒均锁定，断开电键，使磁感应强度均匀增加，经时间t=0.1s磁感应强度大小变为2B此时金属棒甲所受的安培力大小刚好等于金属棒甲的重力，则锁定时两金属棒之间的间距x应为多大？

Answer 1

【答案】(1) 0.4N；(2) 5m/s；(3)

【解析】

(1)金属棒甲匀速运动时，由力的平衡条件可知：

F=m甲g+BI甲L

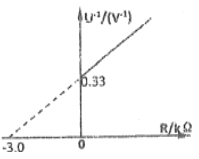
由题图可知流过金属棒乙的电流大小应为：

金属棒乙刚好处于静止状态，由平衡条件可知：

由以上整理得：

F=m甲g+2m乙g

代入数据解得：

F=0.4N；

(2)金属棒乙锁定，闭合电键，金属棒甲向上匀速运动时，有

E甲=BLv1

由闭合电路的欧姆定律得：

对金属棒乙，由平衡条件可知：

BI甲L=2BI乙L=2m乙g

解得：

将金属棒甲锁定，金属棒乙匀速时，有：

解得：

联立解得：

v2=5m/s；

(3)由法拉第电磁感应定律得：

由闭合电路的欧姆定律得：

由题意可知：

m甲g=2BIL

联立以上可得：

解得：

代入数据得：

。