��Ŀ����
����Ŀ����ͼ��ʾ��ij������������Ϊm1=100 kg�Ļ������Ϊ�ʵ㣩�Ӹߴ����������棬Ϊ�����������淢��ײ���������ù̶��ڵ���Ĺ⻬�ķ�֮һԲ�����ʹ�����й���������ٻ��£�����뾶R=1.8 m�������Ͻ�����������ŷ�������ȫ��ͬ��ľ��A��B�����Ⱦ�Ϊ![]() =2m��������Ϊm2=100 kg��ľ���ϱ�������ĩ�����С�������ľ���Ķ�Ħ������Ϊ
=2m��������Ϊm2=100 kg��ľ���ϱ�������ĩ�����С�������ľ���Ķ�Ħ������Ϊ![]() 1��ľ��������Ķ�Ħ������
1��ľ��������Ķ�Ħ������![]() =0.2�������Ħ�����뻬��Ħ������С��ȣ�ȡg=10 m/s2��
=0.2�������Ħ�����뻬��Ħ������С��ȣ�ȡg=10 m/s2��
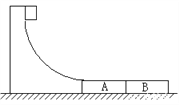
��1�������ﻬ��ľ��Aʱ��ľ�岻����������ľ��Bʱ��ľ��B��ʼ��������![]() 1Ӧ�����������
1Ӧ�����������
��2����![]() ������ﻬ��ľ��Aĩ��ʱ���ٶȺ���ľ��A���˶���ʱ�䡣
������ﻬ��ľ��Aĩ��ʱ���ٶȺ���ľ��A���˶���ʱ�䡣
���𰸡���1��![]() ��2��0.4s
��2��0.4s
����������1��������ľ��Aʱ��ľ�岻������������������1m1g�ܦ�2��m1+2m2 ��g ��
������ľ��Bʱ��ľ��B��ʼ��������������������1m1g����2��m1+m2 ��g ��
�����������ݵ�0.4����1��0.6��
��2������ﻬ��Բ���ĩ���ǵ��ٶ�Ϊv0���Ի�����»������и��ݻ�е���غ㶨�ɵã�mgR=![]() m1v02��
m1v02��
����1=0.5ʱ�������Ͽ�֪��������ľ��A�ϻ���ʱ��ľ�岻����
�������ľ��A���������˶�ʱ�ļ��ٶȴ�СΪa1����ţ�ٵڶ����ɵ� ��1m1g=m1a1
����ﻬ��ľ��Aĩ���ǵ��ٶ�Ϊv1�����˶�ѧ��ʽ��v12-v02=-2a1L
�����������ݵ� v1=4m/s
����ľ��A���˶���ʱ��Ϊt�����˶�ѧ��ʽ�� v1=v0-a1t
�����������ݵ� t=0.4s��

 ������ҵ��ͬ����ϰ��ϵ�д�
������ҵ��ͬ����ϰ��ϵ�д�