题目内容
【题目】（5分）如图所示，一个质量为m=2 kg的物块，在F=10 N的拉力作用下，从静止开始沿水平面做匀加速直线运动，拉力方向与水平成θ=37°，物块与水平面的动摩擦因数μ=0.5，取重力加速度g=10 m/s2，sin 37°=0.6，cos 37°=0.8。
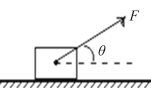
（1）画出物块的受力示意图；
（2）此物块所受到的滑动摩擦力为多大；
（3）求此物块在2 s末的速度。
【答案】（1）物块的受力示意图如下 （2）7 N （2）1 m/s
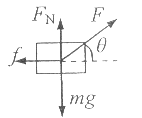
【解析】（1）物块受到重力、拉力、支持力和滑动摩擦力，物块的受力示意图如下。
（1分）
（2）物块竖直方向受力平衡，则有：
Fsin 37°+FN=mg
解得：FN=mg–Fsin 37°（1分）
此物块所受到的滑动摩擦力为：
f=μFN=μ(mg–Fsin 37°)
代入数据解得：f=7 N（1分）
（3）根据牛顿第二定律，有：
Fcos 37°–f=ma（1分）
代入数据解得：a=0.5 m/s2
所以物块在2 s末的速度为：
v=at=0.5×2 m/s=1 m/s（1分）
练习册系列答案
相关题目
