题目内容
【题目】如图所示,匀速转动的水平转台上,沿半径方向放置两个用细线相连的小物块A、B(可视为质点),质量分别为![]() kg、
kg、![]() kg;细线长
kg;细线长![]() m,A、B与转台间的动摩擦因数
m,A、B与转台间的动摩擦因数![]() 。开始转动时A放在转轴处,细线刚好拉直但无张力, 重力加速度
。开始转动时A放在转轴处,细线刚好拉直但无张力, 重力加速度![]() m/s2。最大静摩擦力等于滑动摩擦力,求:
m/s2。最大静摩擦力等于滑动摩擦力,求:
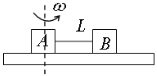
(1)使细线刚好拉直但无张力,转台转动的最大角速度![]() 为多少;
为多少;
(2)使A、B能随转台一起匀速圆周运动,转台转动的最大角速度![]() 为多少
为多少
【答案】(1)1 rad/s;(2)2 rad/s。
【解析】
试题分析:(1)当转台角速度为ω1时,B与转台间摩擦力恰好达最大静摩擦力,细绳的弹力刚好为零;有:![]() 代入数值解得:ω1=1 rad/s。
代入数值解得:ω1=1 rad/s。
(2)当转台角速度为ω2时,A、B与转台间摩擦力都达最大静摩擦力,则:
对A有:![]() ;
;
对B有:![]()
代入数值解得:ω2=2 rad/s。

练习册系列答案
相关题目