题目内容
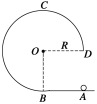
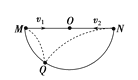
【题目】如图所示为一半球形的坑,其中坑边缘两点M、N刚好与圆心等高。现甲、乙两位同学分别站在M、N两点同时将两个小球以v1、v2的速度沿如图所示的方向抛出,发现两球刚好落在坑中同一点Q,已知∠MOQ=60°,忽略空气的阻力。则下列说法正确的是( )
A. ![]()
B. 同时增大v1、v2,则两球落在坑中时,落地点位于Q点的右侧
C. 两球的初速度无论怎样变化,只要落在坑中的同一点,v1+v2就为常数
D. 若仅增大v1,则两球可在落在坑中前相遇
【答案】AD
【解析】A、根据几何关系知,Q到O点的水平方向的距离等于![]() ,所以M的水平位移
,所以M的水平位移![]() ,N的水平位移
,N的水平位移![]() ,则落在Q点的水平位移之比为
,则落在Q点的水平位移之比为![]() ,运动时间相等,则初速度之比为
,运动时间相等,则初速度之比为![]() ,故A正确;
,故A正确;
B、若要使两小球落在P点右侧的弧面上同一点,则A球水平方向位移增大,B球水平位移减小,而两球运动时间相等,所以应使![]() 增大,
增大, ![]() 减小,故B错误;
减小,故B错误;
C、要两小球落在弧面上的同一点,则水平位移之和为![]() ,则
,则![]() ,落点不同,竖直方向位移就不同,t也不同,所以
,落点不同,竖直方向位移就不同,t也不同,所以![]() 也不是一个定值,故C错误;
也不是一个定值,故C错误;
D、若只增大![]() ,而
,而![]() 不变,则M运动的轨迹的落点将向右一些,两球可在空中相遇,故D正确。
不变,则M运动的轨迹的落点将向右一些,两球可在空中相遇,故D正确。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目