Question

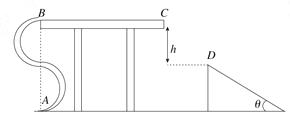
【题目】如图所示，用内壁光滑的薄壁细管弯成的“S”形轨道固定于竖直平面内，弯曲部分是由两个半径均为R＝0.2 m的半圆平滑对接而成(圆的半径远大于细管内径)。轨道底端A与水平地面相切，顶端与一个长为l＝0.9 m的水平轨道相切B点。一倾角为θ＝37°的倾斜轨道固定于右侧地面上，其顶点D与水平轨道的高度差为h＝0.45 m，并与其他两个轨道处于同一竖直平面内。一质量为m＝0.1 kg的小物体(可视为质点)在A点被弹射入“S”形轨道内，沿轨道ABC运动，并恰好从D点以平行斜面的速度进入倾斜轨道。小物体与BC段间的动摩擦因数μ＝0.5。(不计空气阻力，g取10 m/s2。sin37°＝0.6, cos37°＝0.8)

（1）小物体从B点运动到D点所用的时间；

（2）小物体运动到B点时对“S”形轨道的作用力大小和方向；

Answer 1

【答案】（1）0.5 s （2）11.5 N, 方向向上

【解析】试题分析：（1）小物体从C到D做平抛运动有：，

解得：，

物体从B到C做匀减速运动，由牛顿第二定律得

，，

解得：

小物体从B点运动到D点所用的时间：

（2）物体运动到B点受到向下的弹力，由牛顿第二定律得

解得：

由牛顿第三定律有：，故

所以对“S”形轨道的作用力大小为11.5 N，方向向上。