��Ŀ����
20��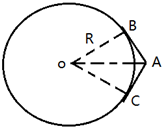 �ҹ������з����Ÿ߷ֱ��ʶԵع۲����ǡ��߷�һ�š�����2013��4��12���ɳ������Ŷ����ػ���������գ�2013��12����ʽͶ��ʹ�ã������ǶԵ�������ķֱ��ʿɴ�2�ף��ɶ�ȫ�����ɨ�����㣬�ﵽ��������Ƚ�ˮƽ���衰�߷�һ�š������Ƶ�����ϱ�����������Բ���˶����Ե�����Ž�Ϊ120�㣬��ͼ��ʾ��������A�㣮��֪������������ٶ�Ϊg������İ뾶ΪR��������������ΪG����
�ҹ������з����Ÿ߷ֱ��ʶԵع۲����ǡ��߷�һ�š�����2013��4��12���ɳ������Ŷ����ػ���������գ�2013��12����ʽͶ��ʹ�ã������ǶԵ�������ķֱ��ʿɴ�2�ף��ɶ�ȫ�����ɨ�����㣬�ﵽ��������Ƚ�ˮƽ���衰�߷�һ�š������Ƶ�����ϱ�����������Բ���˶����Ե�����Ž�Ϊ120�㣬��ͼ��ʾ��������A�㣮��֪������������ٶ�Ϊg������İ뾶ΪR��������������ΪG������1�����߷�һ�š������Ƶ���������Բ���˶����ٶ�Ϊ���
��2����Ҫ��һ���ʱ���ڣ���T0��ʾ���Ե������ȫ��ɨ�裬��ֻ������̫�����յIJ��ֽ���ɨ�裬����ÿ��ɨ��Ŀ������ٶ��
���� ��1������ͼʾ�ɼ��ι�ϵȷ�������Ƶ���Բ���˶��Ĺ���뾶���ٸ������������ṩԲ���˶��������͵�����������������������������������ٶȣ�
��2���ɵ�����ת���ٶ�����������е���һ�ܵ�ʱ���ڣ�����ת����Բ�Ľǣ��ٸ��ݻ�����Բ�ĽǵĹ�ϵ��⣮
��� �⣺��1����ͼʾ���ι�ϵ�У��������Ƶ���Բ���˶��Ĺ���뾶r=$\frac{R}{sin\frac{120��}{2}}$=$\frac{2\sqrt{3}}{3}R$
�ڵ�������������������������У�$G\frac{mM}{{R}^{2}}=mg$
�ɵ�GM=gR2
�����������ṩԲ���˶���������$G\frac{mM}{{r}^{2}}=m\frac{{v}^{2}}{r}$
�ɵ����ǵ��ٶ�v=$\sqrt{\frac{GM}{r}}=\sqrt{\frac{g{R}^{2}}{\frac{2\sqrt{3}}{3}R}}$=$\sqrt{\frac{\sqrt{3}}{2}}\sqrt{gR}$
��2���������������ṩԲ���˶��������У�
$G\frac{mM}{{r}^{2}}=mr\frac{4{��}^{2}}{{T}^{2}}$
�ɵ����ǵ�����T=$\sqrt{\frac{4{��}^{2}{r}^{3}}{GM}}=2��\sqrt{\frac{��\frac{2\sqrt{3}}{3}R��^{3}}{g{R}^{2}}}$
������ת���ٶ�Ϊ��=$\frac{2��}{{T}_{0}}$
���������е���һ�ܵ�ʱ��T�ڣ�����ת����Բ�Ľ�Ϊ
��=��T=$\frac{2��}{{T}_{0}}$T ��
��ô�����ת��������Ϸ�ʱ����Բ�ܵĻ���Ϊs=��R=$R\frac{2��}{{T}_{0}}T$=$\frac{8{��}^{2}R}{3{T}_{0}}\sqrt{\frac{2\sqrt{3}R}{g}}$��
�𣺣�1�����߷�һ�š������Ƶ���������Բ���˶����ٶ�Ϊ$\sqrt{\frac{\sqrt{3}}{2}}\sqrt{gR}$��
��2����Ҫ��һ���ʱ���ڣ���T0��ʾ���Ե������ȫ��ɨ�裬��ֻ������̫�����յIJ��ֽ���ɨ�裬����ÿ��ɨ��Ŀ�������Ϊ$\frac{8{��}^{2}R}{3{T}_{0}}\sqrt{\frac{2\sqrt{3}R}{g}}$��
���� �������Ĺؼ�һ�Ǹ��ݼ��ι�ϵ������ǹ���뾶�����Ǹ�������������������ȼ����������ṩԲ���˶��������������ǵ����ٶ������ڵ���������

| A�� | �������˵�ѹ����Чֵ��Ϊ28.2 V | B�� | �������Ƶ�ʱ�Ϊ100 Hz | ||
| C�� | �������ĵĹ��ʽ���Ϊ20 W | D�� | �������ĵĹ��ʽ���Ϊ40 W |
| A�� | ��ƽ���˶������壬ÿ�����ٶȵĸı���һ����� | |
| B�� | ��Բ���˶������壬���ܺ������ķ���һ�����ٶȷ���ֱ | |
| C�� | ��Բ���˶������壬���ٶȵķ���һ�����ٶȷ���ֱ | |
| D�� | ��Բ���˶������壬���ܵĺ���������Բ���˶������������ |

| A�� | 2sĩ�����忪ʼ�ı��˶����� | |
| B�� | 6sĩ������ص������� | |
| C�� | 0-2sʱ���ڼס����������ƽ���ٶ���ͬ | |
| D�� | 2sĩ�ס������������� |
| A�� | ���ȼ����߶������ȼ���ǰ�������߶Եؼ��ٶȴ�С��� | |
| B�� | �������߶���������ǰ�����˺ͳ��Ե�λ�ƴ�С�������ɷ��� | |
| C�� | ����������ߣ�����ʱ���˺ͳ��ܶ�����ͬ | |
| D�� | ��ֹͣ�߶�ʱ�������ٶȲ�һ��Ϊ�� |
| A�� | ���渽���������ܵ����������������� | |
| B�� | ���������ڵ��渽���������ܵ����������������� | |
| C�� | �ڲ�̫��ȷ�ļ����У�������Ϊ������������������ | |
| D�� | �ϸ�˵������������������������������������������������������⣬�ڵ���������������������С���������� |
| A�� | �Ƶ��������ٶȴ���7.9km/s | |
| B�� | �����߶�һ������Ե��澲ֹ | |
| C�� | ���ļ��ٶ��뾲ֹ�ڳ������������ļ��ٶȴ�С��� | |
| D�� | �Ƶ������еĽ��ٶȱ������Ƶ������еĽ��ٶ�С |

 ��ͼ����ƽ��ֱ������ϵxOy�У�ONΪ��x��ˮƽ���õ�ӫ���������Ϸ���Ϊh��������ڴ��ڴ�ֱ����ƽ���������ǿ�ų���������ڴ�����y�Ḻ�������ǿ�糡����ˮƽ��PQΪ����ֽ��棬A��y���������ϵ�һ�㣬��������ԭ��O�ľ���Ϊ2h������Ϊm�������Ϊq�������Ӵ�A�����ٶ�v0��ֱ��y������糡�����Ӿ�PQ�����ϵ�C����x��������ɦ�=60������ų����պô�ֱ����ӫ�����ϵ�D�㣮�������ӵ���������
��ͼ����ƽ��ֱ������ϵxOy�У�ONΪ��x��ˮƽ���õ�ӫ���������Ϸ���Ϊh��������ڴ��ڴ�ֱ����ƽ���������ǿ�ų���������ڴ�����y�Ḻ�������ǿ�糡����ˮƽ��PQΪ����ֽ��棬A��y���������ϵ�һ�㣬��������ԭ��O�ľ���Ϊ2h������Ϊm�������Ϊq�������Ӵ�A�����ٶ�v0��ֱ��y������糡�����Ӿ�PQ�����ϵ�C����x��������ɦ�=60������ų����պô�ֱ����ӫ�����ϵ�D�㣮�������ӵ���������