题目内容
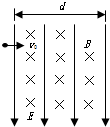 如图所示,匀强电场方向竖直向下,匀强磁场方向垂直纸面向里.已知该正交电磁场区域的宽度d=8cm,带电粒子以速度v0水平向右射入该正交电磁场区域时,恰好不改变运动方向.若粒子射入时,只有电场,测得该带电粒子沿竖直方向向上偏移y1=3.2cm.不计带电粒子的重力,若粒子射入时只有磁场.求带电粒子离开磁场时偏离原方向的距离y2.
如图所示,匀强电场方向竖直向下,匀强磁场方向垂直纸面向里.已知该正交电磁场区域的宽度d=8cm,带电粒子以速度v0水平向右射入该正交电磁场区域时,恰好不改变运动方向.若粒子射入时,只有电场,测得该带电粒子沿竖直方向向上偏移y1=3.2cm.不计带电粒子的重力,若粒子射入时只有磁场.求带电粒子离开磁场时偏离原方向的距离y2.分析:若撤去磁场,粒子做类平抛运动,运用运动的分解,由水平位移和竖直位移研究电场强度与磁感应强度的关系.若撤去电场,粒子做匀速圆周运动,由牛顿第二定律求出半径,由几何知识求出穿过场区后的侧移.
解答:解:设带电粒子带电量为q,质量为m,电场强度为E,磁感应强度为B.
在电磁场中,带电粒子恰好没有偏转,说明其做匀速直线运动,则有:Bqv0=qE …①
只有电场时,做类平抛运动:
t=
…②
y1=
at2=
?
?t2…③
只有磁场时,做匀速圆周运动,洛仑兹力提供向心力,Bqv0=m
…④
由①~④解得:r=
=10cm>8cm,带电粒子从场区右则射出磁场
由几何关系得:y2=r-
=4cm
答:带电粒子离开磁场时偏离原方向的距离y2为4cm.
在电磁场中,带电粒子恰好没有偏转,说明其做匀速直线运动,则有:Bqv0=qE …①
只有电场时,做类平抛运动:
t=
| d |
| v0 |
y1=
| 1 |
| 2 |
| 1 |
| 2 |
| qE |
| m |
只有磁场时,做匀速圆周运动,洛仑兹力提供向心力,Bqv0=m
| v02 |
| r |
由①~④解得:r=
| d2 |
| 2y1 |
由几何关系得:y2=r-
| r2-d2 |
答:带电粒子离开磁场时偏离原方向的距离y2为4cm.
点评:本题是速度选择器模型、电偏转和磁偏转的综合,要注意两种偏转研究方法的不同,电偏转运用运动的合成与分解,磁偏转画轨迹,根据几何关系结合洛仑兹力提供向心力列方程求解.

练习册系列答案
相关题目
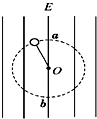 如图所示,在竖直方上的匀强电场中,一根不可伸长的绝缘细绳的一端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b.不计空气阻力,则( )
如图所示,在竖直方上的匀强电场中,一根不可伸长的绝缘细绳的一端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b.不计空气阻力,则( )| A、小球一定带正电 | B、电场力跟重力平衡 | C、小球在从a点运动到b点的过程中,电势能一定增大 | D、小球在运动过程中机械能守恒 |
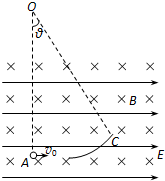 在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4 kg、电荷量q=+9.0×10-4 C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,求:
在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4 kg、电荷量q=+9.0×10-4 C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,求:



 (3)粒子在电、磁场中运动的总时间。
(3)粒子在电、磁场中运动的总时间。