题目内容
【题目】如图所示,电源电动势E=64V,内阻不计,电阻![]() ,开始开关
,开始开关![]() 闭合,
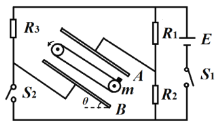
闭合,![]() 断开,平行板电容器的两极板A、B与水平面的夹角
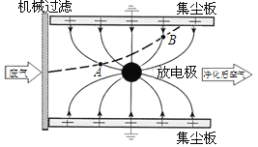
断开,平行板电容器的两极板A、B与水平面的夹角![]() ,两极板A、B间的距离d=0.4m,板间有一个传动装置,绝缘传送带与极板平行,皮带传动装置两轮轴心相距L=1m,传送带逆时针匀速转动,其速度为v=4m/s,现有一个质量m=0.1kg、电荷量q=+0.02C的工件(可视为质点,电荷量保持不变)轻放在传送带底端,工件与传送带间的动摩擦因数μ=0.25.同时开关
,两极板A、B间的距离d=0.4m,板间有一个传动装置,绝缘传送带与极板平行,皮带传动装置两轮轴心相距L=1m,传送带逆时针匀速转动,其速度为v=4m/s,现有一个质量m=0.1kg、电荷量q=+0.02C的工件(可视为质点,电荷量保持不变)轻放在传送带底端,工件与传送带间的动摩擦因数μ=0.25.同时开关![]() 也闭合,极板间电场反向,电路瞬间能稳定下来。(
也闭合,极板间电场反向,电路瞬间能稳定下来。(![]() ,sin37°=0.6,cos37°=0.8)求:
,sin37°=0.6,cos37°=0.8)求:
(1)开关![]() 闭合,
闭合,![]() 断开时,两极板A、B间的场强大小和方向;
断开时,两极板A、B间的场强大小和方向;
(2)工件在传送带上运动的加速度大小;
(3)工件从底端运动到顶端过程中,工件因与传送带摩擦而产生的热量.
【答案】(1)40V/m,电场方向为由B指向A;(2)![]() (3)2.4J
(3)2.4J
【解析】
由闭合电路的欧姆定律求出开关S1闭合,S2断开时,两极板A、B间的电压,然后由![]() 即可求出场强;同(1)求出开关S2也闭合后AB之间的电压和场强,求出工件受到的合力,然后使用牛顿第二定律求出加速度;使用运动学的公式,求出工件从底端运动到顶端的过程中相对于传送带的位移,然后用Q=fL相对求出工件与传动带因摩擦而产生的热量;
即可求出场强;同(1)求出开关S2也闭合后AB之间的电压和场强,求出工件受到的合力,然后使用牛顿第二定律求出加速度;使用运动学的公式,求出工件从底端运动到顶端的过程中相对于传送带的位移,然后用Q=fL相对求出工件与传动带因摩擦而产生的热量;
解:(1)开关S1闭合,S2断开时,R1与R2串联,电路中的电流:![]()
此时A、B之间的电势差等于R1两端的电压,
所以:![]()
两极板A、B间的场强大小:![]()
电场方向为由B指向A;
(2)开关S2也闭合,R1与R2串联电压不变,所以流过它们的电流不变,此时A、B之间的电势差等于R2两端的电压,所以:![]()
两极板A、B间的场强大小:![]()
此时工件的受力如图,则沿传送带的方向由牛顿第二定律得:![]()
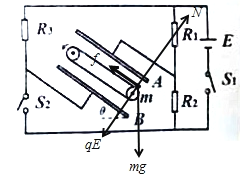
垂直于传送带的方向:![]()
![]()
![]()
(3)工件达到4m/s需要的时间:![]()
工件的位移:![]()
所以工件应该一直做加速运动,![]()
![]()
此时传送带的位移:![]()
工件相对于传送带的位移:![]()
工件与传动带因摩擦而产生的热量:![]()