题目内容
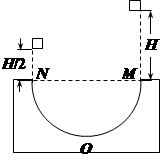
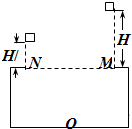 一粗糙半圆轨道MN竖直放置,直径MN位于水平,如图所示,一小物块从M点正上方高H处自由下落,正好滑入半圆轨道,它离开N点后上升的高度为
一粗糙半圆轨道MN竖直放置,直径MN位于水平,如图所示,一小物块从M点正上方高H处自由下落,正好滑入半圆轨道,它离开N点后上升的高度为| H |
| 2 |
| A、正好到达M点,然后回滑 |
| B、到不了M点即回滑 |
| C、可冲出M点再上升一段高度 |
| D、不能确定能否冲出M点 |
分析:根据动能定理求解质点在槽中滚动摩擦力做功;除重力之外的力做功量度物体机械能的变化;第二次小球在槽中滚动时,对应位置处速度变小,因此槽给小球的弹力变小,摩擦力变小,摩擦力做功变小.
解答:解:质点第一次在槽中滚动过程,由动能定理得:
mg(H-
)+(-Wf)=0-0
(Wf为质点克服摩擦力做功大小)
解得:Wf=
mgH
即第一次质点在槽中滚动损失的机械能为
mgH;
由于第二次小球在槽中滚动时,对应位置处速度变小,因此槽给小球的弹力变小,摩擦力变小,摩擦力做功小于
mgH,机械能损失小于
mgH,因此小球再次冲出a点时,能上升的高度大于零而小于
H;
故ABD错误,C正确;
故选:C.
mg(H-
| H |
| 2 |
(Wf为质点克服摩擦力做功大小)
解得:Wf=
| 1 |
| 2 |
即第一次质点在槽中滚动损失的机械能为
| 1 |
| 2 |
由于第二次小球在槽中滚动时,对应位置处速度变小,因此槽给小球的弹力变小,摩擦力变小,摩擦力做功小于
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故ABD错误,C正确;
故选:C.
点评:动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.摩擦力做功使得机械能转化成内能.

练习册系列答案
相关题目