题目内容
 如图所示,在一条平直的公路上有等间距的五个点A、B、C、D、E,相邻两点间距离为L=30m.一辆汽车在公路上做匀加速直线运动,经过这五个点,已知汽车(车头最前端)通过AB段和BC段所用时间分别为3s和2s.由此可求得:
如图所示,在一条平直的公路上有等间距的五个点A、B、C、D、E,相邻两点间距离为L=30m.一辆汽车在公路上做匀加速直线运动,经过这五个点,已知汽车(车头最前端)通过AB段和BC段所用时间分别为3s和2s.由此可求得:(1)汽车的加速度a的大小为
(2)汽车(车头最前端)经过E点时刻的速度大小为
分析:(1)匀变速直线运动某段时间内的平均速度等于中间时刻的瞬时速度,根据该规律求出
段和
段中间时刻的瞬时速度,根据速度时间公式求出汽车的加速度大小.
(2)根据速度时间公式先求出汽车(车头最前端)经过A点时的速度,然后使用导出公式求出汽车经过E点时刻的速度vE的大小.
. |
| AB |
. |
| BC |
(2)根据速度时间公式先求出汽车(车头最前端)经过A点时的速度,然后使用导出公式求出汽车经过E点时刻的速度vE的大小.
解答:解:(1)
段的平均速度
=
=
m/s=10m/s,
段的平均速度
=
=
m/s=15m/s
a=
=
m/s2=2m/s2.
(2)AB段中间时刻距A点的时间为1.5s.
则A点速度vA=v1-at1=7 m/s
由导出公式:2as=v2-
所以E点的速度:v=
=
m/s≈23m/s
故答案为:(1)2m/s2,(2)23m/s
. |
| AB |
. |
| v1 |
| ||
| t1 |
| 30 |
| 3 |
. |
| BC |
. |
| v2 |
| ||
| t2 |
| 30 |
| 2 |
a=
| ||||
|
| 15-10 |
| 1.5+1 |
(2)AB段中间时刻距A点的时间为1.5s.
则A点速度vA=v1-at1=7 m/s
由导出公式:2as=v2-
| v | 2 A |
所以E点的速度:v=
2as+
|
| 2×2×4×30+72 |
故答案为:(1)2m/s2,(2)23m/s
点评:解决本题的关键掌握匀变速直线运动的规律,会灵活运用运动学公式进行求解.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
 如图所示,在一条平直的公路上有等间距的五个点A、B、C、D、E,相邻两点间距离为L=30m.一辆汽车在公路上做匀加速直线运动,在加速过程中经过这五个点,已知汽车(车头最前端)通过
如图所示,在一条平直的公路上有等间距的五个点A、B、C、D、E,相邻两点间距离为L=30m.一辆汽车在公路上做匀加速直线运动,在加速过程中经过这五个点,已知汽车(车头最前端)通过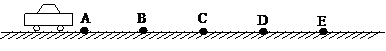
 ,相邻两点间距离为L=30m。一辆汽车在公路上做匀加速直线运动,经过这五个点,已知汽车(车头最前端)通过
,相邻两点间距离为L=30m。一辆汽车在公路上做匀加速直线运动,经过这五个点,已知汽车(车头最前端)通过 段和
段和 段所用时间分别为
段所用时间分别为 和
和 。试求:
。试求: 
 的大小;
的大小; 点时刻的速度V的大小。
点时刻的速度V的大小。 所用时间。
所用时间。