题目内容
 如图所示,在一条平直的公路上有等间距的五个点A,B,C,D,E,相邻两点间距离为L=30m.一辆汽车在公路上做匀加速直线运动,经过这五个点,已知汽车(车头最前端)通过AB段和BC段所用时间分别为3s和2s.试求:
如图所示,在一条平直的公路上有等间距的五个点A,B,C,D,E,相邻两点间距离为L=30m.一辆汽车在公路上做匀加速直线运动,经过这五个点,已知汽车(车头最前端)通过AB段和BC段所用时间分别为3s和2s.试求:(1)汽车的加速度a的大小;
(2)汽车(车头最前端)经过E点时刻的速度V的大小.
(3)汽车(车头最前端)经过BE所用时间.
分析:(1)汽车在公路上做匀加速直线运动,根据推论可分别求出AB段和BC段中间时刻的速度,再由加速度的定义式求出加速度.
(2)由速度公式求汽车经过B点时刻的速度的大小,再由位移速度关系式求解经过E点时刻的速度V的大小.
(3)根据平均速度求出汽车(车头最前端)经过BE所用时间.
(2)由速度公式求汽车经过B点时刻的速度的大小,再由位移速度关系式求解经过E点时刻的速度V的大小.
(3)根据平均速度求出汽车(车头最前端)经过BE所用时间.
解答:解:(1)汽车在公路上做匀加速直线运动,由推论则有:
AB中间时刻的速度:V1=
=10m/s
BC中间时刻的速度V2=
=15m/s
则其加速度为 a=
=2.0m/s2
(2)B点速度VB=V1+at=13.0m/s
则经过E点时刻的速度V的大小为V=
=23.0m/s.
(3)汽车(车头最前端)经过BE所用时间为
tBE=
=
=5.0s
答:(1)汽车的加速度a的大小是2m/s2;
(2)汽车(车头最前端)经过E点时刻的速度V的大小为23m/s.
(3)汽车(车头最前端)经过BE所用时间是5s.
AB中间时刻的速度:V1=
| L |
| t1 |
BC中间时刻的速度V2=
| L |
| t2 |
则其加速度为 a=
| V2-V1 |
| △t |
(2)B点速度VB=V1+at=13.0m/s
则经过E点时刻的速度V的大小为V=
|
(3)汽车(车头最前端)经过BE所用时间为
tBE=
| 3L | ||
|
| 3L | ||
|
答:(1)汽车的加速度a的大小是2m/s2;
(2)汽车(车头最前端)经过E点时刻的速度V的大小为23m/s.
(3)汽车(车头最前端)经过BE所用时间是5s.
点评:对于运动学问题,首先要明确物体的运动性质,其次在分析已知条件的基础上,灵活选择公式求解.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 如图所示,在一条平直的公路上有等间距的五个点A、B、C、D、E,相邻两点间距离为L=30m.一辆汽车在公路上做匀加速直线运动,在加速过程中经过这五个点,已知汽车(车头最前端)通过
如图所示,在一条平直的公路上有等间距的五个点A、B、C、D、E,相邻两点间距离为L=30m.一辆汽车在公路上做匀加速直线运动,在加速过程中经过这五个点,已知汽车(车头最前端)通过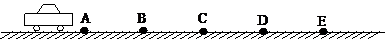
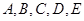 ,相邻两点间距离为L=30m。一辆汽车在公路上做匀加速直线运动,经过这五个点,已知汽车(车头最前端)通过
,相邻两点间距离为L=30m。一辆汽车在公路上做匀加速直线运动,经过这五个点,已知汽车(车头最前端)通过 段和
段和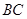 段所用时间分别为
段所用时间分别为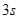 和
和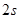 。试求:
。试求: 
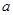 的大小;
的大小; 点时刻的速度V的大小。
点时刻的速度V的大小。 所用时间。
所用时间。