题目内容
17. 空间一均匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标(0,a,0),N点的坐标为(a,0,0)(a,0,0),P点的坐标为(a,$\frac{a}{2}$,$\frac{a}{2}$).已知电场方向平行于直线MN,M点电势为0,N点电势为4V,则把一个电荷量q=10-5C的正电荷从P移到M,电场力做的功为-1×10-5J.
空间一均匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标(0,a,0),N点的坐标为(a,0,0)(a,0,0),P点的坐标为(a,$\frac{a}{2}$,$\frac{a}{2}$).已知电场方向平行于直线MN,M点电势为0,N点电势为4V,则把一个电荷量q=10-5C的正电荷从P移到M,电场力做的功为-1×10-5J.
分析 将电场强度沿坐标轴方向正交分解,求出轴向的E的分量值,再选用U=Ed,求得PM间的电势差,再由公式W=qU求电场力做功.
解答 解:根据题意已知电场方向平行于直线MN,点M的电势为0,点N的电势为4V,故
UNM=E•$\sqrt{2}$a=4V ①
将电场强度沿着-x方向和+y方向正交分解,设合场强为E,则-x和+y方向的分量分别为:
Ex=$\frac{\sqrt{2}}{2}$E,Ey=$\frac{\sqrt{2}}{2}$E ②
设P在x0y平面上的投影为P′点,投影点的坐标为:($\frac{a}{2}$,a,0)
则 UMP=UMP′=Ey•$\frac{1}{2}$a=$\frac{\sqrt{2}}{4}$Ea=1V (将①代入得到)
因此 UPM=-UMP=-1V
所以把一个电荷量q=10-5C的正电荷从P移到M,电场力做的功 WPM=qUPM=-1×10-5J
故答案为:-1×10-5J.
点评 本题关键运用正交分解法,将电场沿着坐标轴方向正交分解,然后由U=Ed求解电势差.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
8.如图所示,下列光学现象及其解释正确的是( )
| A. |  图中,漫反射的光线杂乱无章,因此不遵循光的反射定律 | |
| B. |  图中,木工师傅观察木板是否光滑平整利用了光沿直线传播的原理 | |
| C. |  图表示的是远视线的成像情况,应该佩戴凸透镜来矫正 | |
| D. |  图表示太阳光经过三棱镜色散后的色光排列情况 |
9.一辆汽车在水平方向以10m/s的速度作匀速直线运动;当汽车以2m/s2的加速度刹车时,其刹车后6s内位移为( )
| A. | 24 m | B. | 25 m | C. | 30m | D. | 96m |
6. 如图,玻璃中有一个气泡,气泡的形状可看作三棱柱形,截面是等腰三角形,现有一束光从玻璃中入射到气泡上,已知入射光有两种频率.则下列说法正确的是( )
如图,玻璃中有一个气泡,气泡的形状可看作三棱柱形,截面是等腰三角形,现有一束光从玻璃中入射到气泡上,已知入射光有两种频率.则下列说法正确的是( )
 如图,玻璃中有一个气泡,气泡的形状可看作三棱柱形,截面是等腰三角形,现有一束光从玻璃中入射到气泡上,已知入射光有两种频率.则下列说法正确的是( )
如图,玻璃中有一个气泡,气泡的形状可看作三棱柱形,截面是等腰三角形,现有一束光从玻璃中入射到气泡上,已知入射光有两种频率.则下列说法正确的是( )| A. | 光从气泡右侧面出射时向下偏折 | |
| B. | B光从气泡右侧出射时向上偏折 | |
| C. | 频率高的光从气泡右侧面出射后,位置靠下 | |
| D. | 频率高的光从气泡右侧面出射后,位置靠上 |
7.两颗人造地球卫星,都在圆形轨道上运行,它们的质量相等,轨道半径之比$\frac{{r}_{1}}{{r}_{2}}$=2,则它们的动能之比等于( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | 4 |
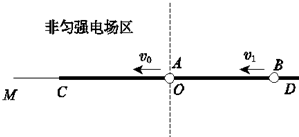 如图所示,虚线左侧存在非匀强电场,MO是电场中的某条电场线,方向水平向右,长直光滑绝缘细杆CD沿该电场线放置.质量为m1、电荷量为+q1的A球和质量为m2、电荷量为+q2的B球穿过细杆(均可视为点电荷).当t=0时A在O点获得向左的初速度v0,同时B在O点右侧某处获得向左的初速度v1,且v1>v0.结果发现,在B向O点靠近过程中,A始终向左做匀速运动.当t=t0时B到达O点(未进入非匀强电场区域),A运动到P点(图中未画出),此时两球间距离最小.静电力常量为k.
如图所示,虚线左侧存在非匀强电场,MO是电场中的某条电场线,方向水平向右,长直光滑绝缘细杆CD沿该电场线放置.质量为m1、电荷量为+q1的A球和质量为m2、电荷量为+q2的B球穿过细杆(均可视为点电荷).当t=0时A在O点获得向左的初速度v0,同时B在O点右侧某处获得向左的初速度v1,且v1>v0.结果发现,在B向O点靠近过程中,A始终向左做匀速运动.当t=t0时B到达O点(未进入非匀强电场区域),A运动到P点(图中未画出),此时两球间距离最小.静电力常量为k.