题目内容
(16分)如图所示,一质量为0.99kg的木块静止在水平轨道AB的B端,水平轨道与半径为10m的光滑弧形轨道BC相切。现有一质量为10g的子弹以500m/s的水平速度从左边射入木块且未穿出。已知木块与水平轨道的动摩擦因数μ=0.5,g=10m/s2。求:
(1)子弹射入木块与木块获得的共同速率;
(2)子弹射入后与木块在圆弧轨道上升的最大高度;
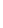 (3)从木块返回B点到静止在水平面上,摩擦阻力的冲量的大小。
(3)从木块返回B点到静止在水平面上,摩擦阻力的冲量的大小。
(1)子弹射入木块与木块获得的共同速率;
(2)子弹射入后与木块在圆弧轨道上升的最大高度;
 (3)从木块返回B点到静止在水平面上,摩擦阻力的冲量的大小。
(3)从木块返回B点到静止在水平面上,摩擦阻力的冲量的大小。
(1)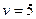 m/s
m/s
(2) m
m
(3)I = 5N·S
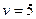 m/s
m/s(2)
 m
m(3)I = 5N·S
(1)(5分)设子弹射入木块与木块获得的共同速度为v,子弹射入木块前后系统动量守恒
 (3分)
(3分)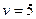 m/s (2分)
m/s (2分)(2)(5分)设木块上升最大高度为h,子弹与木块在光滑弧形轨道BC上运动,到达最高点
的过程中系统机械能守恒
 (3分)
(3分) m (2分)
m (2分)(3)(6分)木块返回B点进入水平轨道上作匀减速运动最终静止,摩擦力的冲量为I,由牛顿第二定律、匀变速运动规律得
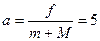 m/s2 (2分)
m/s2 (2分) s (1分)
s (1分) (2分)
(2分)I =" 5N·S " (1分)

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目

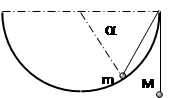


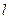 =1.6m,悬点O与地面的距离OC=4m,若空气阻力不计,绳被拉断瞬间小球的机械能无损失。(g=10m/s2)
=1.6m,悬点O与地面的距离OC=4m,若空气阻力不计,绳被拉断瞬间小球的机械能无损失。(g=10m/s2)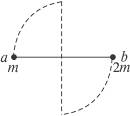


 恒( )
恒( )