��Ŀ����
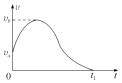
����Ŀ����ͼ�����ΪV���ڱڹ⻬��Բ���ε�����������һ�����ͺ�Ⱦ��ɺ��ԵĻ������������ܷ����¶�Ϊ2.4T0��ѹǿΪ1.2P0���������壮P0��T0�ֱ�Ϊ������ѹǿ���¶ȣ���֪����������U���¶�T�Ĺ�ϵΪU=aT��aΪ���ij�������������������б仯���̶��ǻ����ģ���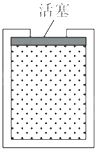
��1������������������ﵽƽ��ʱ�����V1��
��2���ڻ����½������У�����������ų�������Q��
���𰸡�
��1���⣺��������ѹǿP=1.2P0��P0ʱ��V���䣬�¶���2.4T0��ΪT1���ɲ������ɵ� ![]()
�ã�T1=2T0
�������¶���T1��ΪT0�Ĺ����У������V��С��V1������ѹǿ���䣬���Ÿ������˶��ɵ� ![]()
��ã�V1=0.5V
������������������ﵽƽ��ʱ�����Ϊ0.5V
��2�������½������У�����������Ĺ�ΪW=P0��V��V1��
����һ�����У��������ܵļ���Ϊ��U=a��T1��T0��
������ѧ��һ���ɵã�����������ų�������ΪQ=W+��U
�ã�Q= ![]()
���ڻ����½������У�����������ų�������Ϊ ![]() ��
��
����������1������������������ﵽƽ��Ĺ��̣��Ⱦ���һ�ε�����仯���پ���һ�ε�ѹ�仯��������������״̬����������⼴�ɡ�
��2����������ѧ��һ���ɽ�������Ĺ�ʽ����������½������зų���������