جâؤ؟ؤعبف
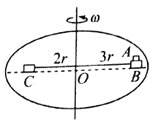
،¾جâؤ؟،؟بçح¼ثùت¾£¬½«ء½¸ِدàح¬µؤ،°U،±ذح¹â»¬½ًتôµ¼¹ى£¬ئ½ذذ·إضأسعز»´إ¸ذس¦ا؟¶ب´َذ،خھB،¢·½دٍ´¹ض±دٍةدµؤشبا؟´إ³،ضذµؤث®ئ½أو£¬ء½µ¼¹ىµؤةد¹ى؛حدآ¹ىثùشعئ½أو¾ùسëث®ئ½أوئ½ذذ£¬ء½µ¼¹ىأوةد¸÷·إز»¸ùحêب«دàح¬µؤضتء؟خھmµؤشبضت½ًتô¸ثQ1؛حQ2£¬از¸ثسë¹ىµہ´¹ض±،£ةèء½µ¼¹ىأودà¾àخھH£¬µ¼¹ى؟يخھL£¬µ¼¹ى×م¹»³¤ازµç×è²»¼ئ£¬½ًتô¸ثµ¥خ»³¤¶بµؤµç×èخھr،£دضسذز»ضتء؟خھ![]() µؤ²»´ّµçذ،اٍزشث®ئ½دٍسزµؤثظ¶بv0ײ»÷¸ثQ1µؤضذµم£¬×²»÷؛َذ،اٍ·´µ¯آنµ½دآ²مأوةدµؤCµم£¬Cµمسë¸ثQ1³ُت¼خ»ضأث®ئ½¾àہëخھs،£اَ£؛
µؤ²»´ّµçذ،اٍزشث®ئ½دٍسزµؤثظ¶بv0ײ»÷¸ثQ1µؤضذµم£¬×²»÷؛َذ،اٍ·´µ¯آنµ½دآ²مأوةدµؤCµم£¬Cµمسë¸ثQ1³ُت¼خ»ضأث®ئ½¾àہëخھs،£اَ£؛

£¨1£©Q1¸ث»ٌµأµؤ×î´َثظ¶ب،£
£¨2£©»طآ·ؤع¸ذس¦µçء÷µؤ×î´َضµ؛حQ2¸ثتـµ½µؤ×î´َ°²إàء¦،£
£¨3£©صû¸ِشث¶¯¹³جضذ¸ذس¦µçء÷×î¶à²ْةْءث¶àةظببء؟،£
،¾´ً°¸،؟£¨1£©![]() £¨2£©
£¨2£©![]() £¬
£¬![]() £¨3£©
£¨3£©![]()
،¾½âخِ،؟
£¨1£©دب¸ù¾فئ½إ×شث¶¯µؤ¹وآةاَ³ِإِ؛َذ،اٍ·´µ¯µؤثظ¶ب،£ذ،اٍײ»÷½ًتô¸ثµؤ¹³ج£¬×ٌتط¶¯ء؟تط؛م¶¨آة،£¸ù¾ف¶¯ء؟تط؛م¶¨آةءذت½£¬´س¶ّاَ³ِ½ًتô¸ث»ٌµأµؤثظ¶ب،£
£¨2£©إِ؛َث²¼ن»طآ·ؤع¸ذس¦µçء÷×î´َ،£سة·¨ہµع¶¨آة؛حإ·ؤ·¶¨آة½ل؛داَ³ِ»طآ·ؤع¸ذس¦µçء÷µؤ×î´َضµ،£شظسةF£½BILاَQ2¸ثتـµ½µؤ×î´َ°²إàء¦،£
£¨3£©إِ؛َ£¬شع°²إàء¦×÷سأدآ£¬½ًتô¸ثA1×ِ¼ُثظشث¶¯£¬½ًتô¸ثA2×ِ¼سثظشث¶¯£¬µ±ء½¸ثثظ¶ب´َذ،دàµبت±£¬»طآ·ؤع¸ذس¦µçء÷خھ0£¬¸ù¾ف¶¯ء؟تط؛م¶¨آة؛حؤـء؟تط؛م¶¨آة½ل؛داَ½âببء؟،£
£¨1£©ةèײ»÷؛َذ،اٍ·´µ¯µؤثظآتخھv£¬½ًتô¸ثQ1µؤ×î´َثظ¶بخھvm£¬ب،ث®ئ½دٍسزخھص·½دٍ£¬¶شسعإِײ¹³ج£¬¸ù¾ف¶¯ء؟تط؛م¶¨آة£¬µأ£؛
![]()
¶شسعذ،اٍµؤئ½إ×شث¶¯£¬¸ù¾فئ½إ×شث¶¯µؤ·ض½â£¬سذ£؛
s=vt
H=![]() gt2،£
gt2،£
سةزشةدبت½½âµأ£؛
![]()
£¨2£©¸ثQ1ثظ¶ب×î´َت±£¬¸ذس¦µç¶¯تئ×î´َ£¬خھ£؛E=BLvm
»طآ·×ـµç×èخھ£؛R=2Lr
ثùزش»طآ·ؤع¸ذس¦µçء÷µؤ×î´َضµخھ£؛![]()
Q2¸ثتـµ½µؤ×î´َ°²إàء¦خھ£؛Fm=BImL
½âµأ£؛
![]()
![]()
£¨3£©زٍخھشع°²إàء¦µؤ×÷سأدآ£¬½ًتô¸ثA1×ِ¼ُثظشث¶¯£¬½ًتô¸ثA2×ِ¼سثظشث¶¯£¬µ±ء½¸ثثظ¶ب´َذ،دàµبت±£¬»طآ·ؤع¸ذس¦µçء÷خھ0£®ةèء½°ô×îضصسذ¹²ح¬ثظ¶بvQ،£ب،ث®ئ½دٍسزخھص·½دٍ£¬سة¶¯ء؟تط؛م¶¨آةµأ£؛
mvm=2mvQ،£
¸ù¾فؤـء؟تط؛م¶¨آةµأ£؛
![]()
½âµأ£؛
![]() ،£
،£

 أد½¨ئ½ذ،ر§¹ِ¶¯²âتشدµءذ´ً°¸
أد½¨ئ½ذ،ر§¹ِ¶¯²âتشدµءذ´ً°¸ »ئ¸شجىجىء·؟عثمجâ؟¨دµءذ´ً°¸
»ئ¸شجىجىء·؟عثمجâ؟¨دµءذ´ً°¸