题目内容
4.已知人造航天器在某行星表面上空绕行星做匀速圆周运动,绕行方向与行星自转方向相同(人造航天器周期小于行星的自转周期),经过时间t(t小于航天器的绕行周期),航天器运动的弧长为s,航天器与行星的中心连线扫过角度为θ,引力常量为G,航天器上的人两次相邻看到行星赤道上的标志物的时间间隔是△t,这个行星的同步卫星的离行星的球心距离( )| A. | $\frac{s△t}{(2πt-θ△t)}$ | B. | $\frac{s△t}{(θ△t-2πt)}$ | ||
| C. | $\frac{s}{θ}\root{3}{{\frac{{{θ^2}△{t^2}}}{{{{(2πt-θ△t)}^2}}}}}$ | D. | $\frac{s}{θ}\root{3}{{\frac{{{θ^2}△{t^2}}}{{{{(θ△t-2πt)}^2}}}}}$ |
分析 对于航天器:s=rθ可求出轨道半径,航天器的角速度为:ω=$\frac{θ}{t}$ 航天器的周期为T=$\frac{2πt}{θ}$,再由两次相重合的条件可表示出同步卫星的周期,再据开普勒第三定律列等式求得同步卫星的轨道半径即为同步卫星的离行星的球心距离.
解答 解:航天器的轨道半径为:r=$\frac{s}{θ}$,航天器的角速度为:ω=$\frac{θ}{t}$ 航天器的周期为T=$\frac{2πt}{θ}$
设同步卫星的周期为T′,则其角速度ω′=$\frac{2π}{T′}$
因时间间隔是△t,则:tω△t-ω′△=2π 得$T′=\frac{2πt△t}{θ△t-2πt}$
又由开普勒第三定律:$\frac{{r}^{3}}{r{′}^{3}}$=$\frac{{T}^{2}}{T{′}^{2}}$可得r′=$\frac{s}{θ}\sqrt{\frac{{θ}^{2}△{t}^{2}}{(θ△t-2πt)^{2}}}$,
故D正确,ABC错误
故选:D
点评 由开普勒第三定律确定周期与半径的关系是解题的关键,明确定再次重合为两者的转过的角度差为2π.

练习册系列答案
相关题目
12. 如图所示,宠物狗在水平地面匀速向前跑动时,主人对绳索的拉力F=l0N,绳索与地面间的夹角θ=37°,己知sin37°=0.6,cos37°=0.8,此时地面对小狗的摩擦力大小是( )
如图所示,宠物狗在水平地面匀速向前跑动时,主人对绳索的拉力F=l0N,绳索与地面间的夹角θ=37°,己知sin37°=0.6,cos37°=0.8,此时地面对小狗的摩擦力大小是( )
 如图所示,宠物狗在水平地面匀速向前跑动时,主人对绳索的拉力F=l0N,绳索与地面间的夹角θ=37°,己知sin37°=0.6,cos37°=0.8,此时地面对小狗的摩擦力大小是( )
如图所示,宠物狗在水平地面匀速向前跑动时,主人对绳索的拉力F=l0N,绳索与地面间的夹角θ=37°,己知sin37°=0.6,cos37°=0.8,此时地面对小狗的摩擦力大小是( )| A. | 4N | B. | 6N | C. | 8N | D. | 10N |
16.有一只标识为“2.5V,0.5A”的小灯泡,小华想测定其伏安特性曲线,实验室所供选择的器材除了导线和开关外,还有以下一些器材可供选择:
(1)为了达到实验目的需要组装一个量程为3.0V的电压表,那么电阻箱的阻值应调到100Ω;
(2)为了减小实验误差,实验中滑动变阻器应选择E(选填器材前面的编号);
(3)请帮助小华设计一个电路,要求使误差尽量小,并将电路图滑在图1虚线框内;
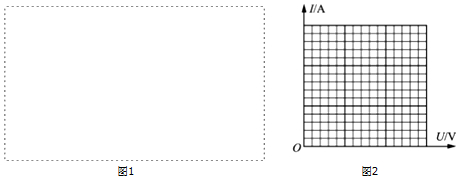
(4)小华在实验中用电流表和改装后的电压表测得数据并记录在下表中,请根据表格中的数据在图2方格纸上作出该小灯泡的伏安特性曲线;
(5)将一个电动势为1.5V,内阻为3Ω的电源直接接在该小灯泡的两端,则该小灯泡的实际功率为0.2W(结果保留1为有效数字).
| 编号 | 器材名称 | 规格与参数 |
| A | 电源E | 电动势为3.0V,内阻不计 |
| B | 电流表A1 | 量程0-10mA,内阻200Ω |
| C | 电流表A2 | 量程0-600mA,内阻2Ω |
| D | 电阻箱R | 阻值999.99Ω |
| E | 滑动变阻器R1 | 最大阻值10Ω |
| F | 滑动变阻器R2 | 最大阻值2kΩ |
(2)为了减小实验误差,实验中滑动变阻器应选择E(选填器材前面的编号);
(3)请帮助小华设计一个电路,要求使误差尽量小,并将电路图滑在图1虚线框内;

(4)小华在实验中用电流表和改装后的电压表测得数据并记录在下表中,请根据表格中的数据在图2方格纸上作出该小灯泡的伏安特性曲线;
| 电压U/V | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| 电流I/A | 0 | 0.17 | 0.30 | 0.39 | 0.45 | 0.49 |
13.关于物理学发展,下列表述正确的有( )
| A. | 伽利略通过“理想斜面”实验得出“力是维持物体运动的原因” | |
| B. | 牛顿发现了万有引力,卡文迪许测出了万有引力常量 | |
| C. | 库仑最先提出了在电场中引入电场线的观点研究电场 | |
| D. | 奥斯特发现了电流的磁效应,总结出了电磁感应定律 |
10.下列说法正确是( )
| A. | 空气的相对湿度可用空气中所含水蒸气的压强来表示 | |
| B. | 由热力学定律知,热量不可以从低温物体传递到高温物体 | |
| C. | 对一定质量的理想气体,气体分子的热运动越剧烈,气体的温度就越高 | |
| D. | 露水总是出现在夜间和清晨,是气温的变化使空气里原来饱和的水蒸气液化的缘故 | |
| E. | 将两个分子由距离极近移动到相距无穷远的过程中,它们的分子势能先减小后增加 |
 如图所示,某棱镜的横截面为直角三角形ABC,其折射率为$\sqrt{3}$,已知∠A=30°、∠C=90°,一束平行于AC的光射向棱镜的左侧界面,经AC面反射后从BC边射出,求:
如图所示,某棱镜的横截面为直角三角形ABC,其折射率为$\sqrt{3}$,已知∠A=30°、∠C=90°,一束平行于AC的光射向棱镜的左侧界面,经AC面反射后从BC边射出,求: 地球上能量的最终来源是太阳光.太阳到地球的平均距离称为一个天文单位,其值r=1.5×1011m,已知在该处单位时间内通过垂直于太阳辐射方向的单位面积的辐射能量E0=1.37×103J•m-2•s-1,光在真空中的传播速度c=3.0×108m/s.则:(以下计算结果均保留一位有效数字).
地球上能量的最终来源是太阳光.太阳到地球的平均距离称为一个天文单位,其值r=1.5×1011m,已知在该处单位时间内通过垂直于太阳辐射方向的单位面积的辐射能量E0=1.37×103J•m-2•s-1,光在真空中的传播速度c=3.0×108m/s.则:(以下计算结果均保留一位有效数字).