��Ŀ����
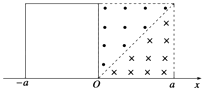
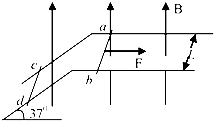
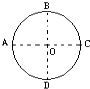
����Ŀ����ͼ��ʾ��xOyƽ���ڰ뾶ΪR��ԲO'��y��������ԭ��O���ڸ�Բ�������ڣ�����y��ƽ�е���ǿ�糡�ʹ�ֱ��Բ�����ǿ�ų���һ����Ϊm�������Ϊq�����ӣ�������������O����x����������ijһ�ٶ����룬��������ǡ��������ֱ���˶�����T0ʱ���P�������
��1��������ȥ�ų������������Դ�O������ͬ���ٶ����룬�� ![]() ʱ��ǡ��Բ������ı߽��������糡ǿ�ȵĴ�С�������뿪�糡ʱ�ٶȵĴ�С��
ʱ��ǡ��Բ������ı߽��������糡ǿ�ȵĴ�С�������뿪�糡ʱ�ٶȵĴ�С��
��2��������ȥ�糡�����������Դ�O�����룬���ٶ�Ϊԭ����2�����������ڴų����˶���ʱ�䣮
���𰸡�
��1���⣺��糡ǿ��ΪE���Ÿ�ǿ��ΪB�����ٶ�Ϊv��ͬʱ���ڵ糡�ʹų�ʱ����������������ֱ���˶��У�
2R=vT0
��ã�
v= ![]()
��ȥ�ų���ֻ���ڵ糡ʱ����������ƽ���˶����У�
x=v ![]()
y= ![]()
![]() ��
�� ![]() ��2
��2
������ʽ�ӿ�֪x=y=R�����Ӵ�ͼ�е�M���뿪�糡��
��ã�
E= ![]()
�֣�vx=v
vy=at= ![]()
![]()
�������뿪�糡ʱ���ٶ�Ϊ��
v= ![]() =
= ![]()
�𣺵糡ǿ�ȵĴ�СΪ ![]() �������뿪�糡ʱ�ٶȵĴ�СΪ
�������뿪�糡ʱ�ٶȵĴ�СΪ ![]() ��
��
��2���⣺ͬʱ���ڵ糡�ʹų�ʱ����������������ֱ���˶��У�
qvB=qE
ֻ���ڴų�ʱ������������Բ���˶�����뾶Ϊr��
q2vB= ![]()
������ʽ�ӿ����r=R����֪�����ڴų����˶� ![]() Բ�ܣ����ԣ������ڴų����˶���ʱ��Ϊ��
Բ�ܣ����ԣ������ڴų����˶���ʱ��Ϊ��
t= ![]() =
= ![]() ��
��
��
T= ![]()
��ã�
t= ![]() =
= ![]() ��
��
��������ȥ�糡�����������Դ�O�����룬���ٶ�Ϊԭ����2�����������ڴų����˶���ʱ��Ϊ ![]() ��
��
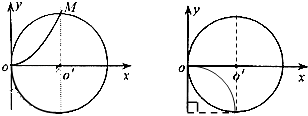
����������1����糡ǿ��ΪE���Ÿ�ǿ��ΪB�����ٶ�Ϊv��ͬʱ���ڵ糡�ʹų�ʱ����������������ֱ���˶����糡������������������ȥ�ų���ֻ���ڵ糡ʱ����������ƽ���˶�������ƽ���˶��Ļ������ɽ�ϼ��ι�ϵ������⣻��2��ֻ���ڴų�ʱ������������Բ���˶����������������ṩ��������ʽ����뾶��������ڹ�ʽ��������˶���ʱ�䣮
�����㾫����������Ĺؼ����������������������֪ʶ��������������ʼ�մ�ֱ��v�ķ���������������һ�����������Լ��Ը�Ӧ�����ķ�������⣬�˽�ͨ�絼���ڴų�������������������ʹŸ��߷����йأ������ֶ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�