题目内容
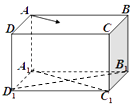
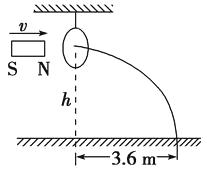
【题目】如图所示,在同一竖直平面内,一轻弹簧一端固定,另一自由端恰好与水平线AB平齐,静止放于倾角为53o的光滑斜面上.一长为L=90cm的轻绳一端固定在O点,另一端系一质量m=1kg的可视为质点的小球,将轻绳拉到水平,使小球从位置C静止释放,小球到达最低点D时,轻绳刚好被拉断.之后小球在运动过程中恰好沿斜面方向将轻弹簧压缩,最大压缩量为x=5cm.已知g=10m/s2 , sin37°=0.6,sin53°=0.8.求: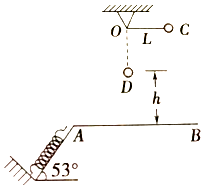
(1)轻绳受到的拉力的最大值;
(2)D点到水平线AB的高度h;
(3)轻弹簧所获得的最大弹性势能.
【答案】
(1)解:从C到D,由机械能守恒可得:
mgL= ![]()
解得:v1= ![]()
在D点,根据牛顿第二定律得:
F﹣mg=m ![]()
代入数据可得:F=3mg=30N
答:细绳受到的拉力的最大值为30 N.
(2)解:从D到A,由平抛运动的规律有
vy2=2gh
tan53°= ![]()
代入数据可得:h=1.6m
答:D点到水平线AB的高度h为1.6m.
(3)解:从C点到将弹簧压缩到最短的过程中,小球与弹簧的机械能守恒得:
Ep=mg(L+h+xsin 53°)
代入数据可得:Ep=25.4J
答:轻弹簧所获得的最大弹性势能为25.4J.
【解析】(1)从C到D,根据机械能守恒定律求出小球在D点的速度,在D点,根据合力提供向心力,运用牛顿第二定律求出绳子的最大拉力.(2)球在运动过程中恰好沿斜面方向将弹簧压缩,知绳子断裂后,做平抛运动,由平抛运动的规律求h.(3)小球从C点到将弹簧压缩至最短的过程中,小球与弹簧系统的机械能守恒,根据系统机械能守恒求出弹簧的最大弹性势能.
【考点精析】根据题目的已知条件,利用动能定理的综合应用和机械能守恒及其条件的相关知识可以得到问题的答案,需要掌握应用动能定理只考虑初、末状态,没有守恒条件的限制,也不受力的性质和物理过程的变化的影响.所以,凡涉及力和位移,而不涉及力的作用时间的动力学问题,都可以用动能定理分析和解答,而且一般都比用牛顿运动定律和机械能守恒定律简捷;在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变.

 阅读快车系列答案
阅读快车系列答案