题目内容
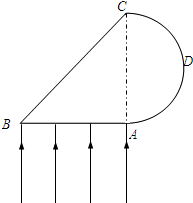
如图所示,ABC为某种透明介质的横截面图,其中△AOC为等腰直角三角形,BC为半径R=10cm的四分之一圆弧,AB与水平屏幕MN垂直并接触于A点.由红光和紫光两种单色光组成的复色光经过BC面射向圆心O,在AB分界面上的入射角i=45°,结果在水平屏幕MN上出现两个亮斑,已知该介质对红光和紫光的折射率分别为n1=
、n2=
.
①判断分布在AM和AN两个区域内亮斑的颜色(写出结果即可);
②求两个亮斑间的距离.
2
| ||
| 3 |
| 2 |
①判断分布在AM和AN两个区域内亮斑的颜色(写出结果即可);
②求两个亮斑间的距离.

①根据临界角公式sinC=
知,C=arcsin
则得 红光与紫光的临界角分别为C红=60°,C紫=45°,
而光线在AB面上入射角i=45°,说明紫光恰好发生了全反射,红光从AB面有反射,也有折射.所以在AM区域的亮斑P1为红色,
在AN区域的亮斑P2为红色与紫色的混合色.
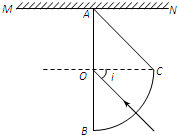
②画出如图光路图.
设折射角为r,两个光斑分别为P1、P2,根据折射定律得
n1=
求得sinr=
由几何知识可得tanr=
解得AP1=7.05×10-2m
由几何知识可得△OAP2为等腰直角三角形,
解得AP2=0.1m
所以P1P2=(5
+10)cm=0.17m
答:①在AM区域的亮斑P1为红色,在AN区域的亮斑P2为红色与紫色的混合色.
②两个亮斑间的距离是0.17m.

| 1 |
| n |
| 1 |
| n |
则得 红光与紫光的临界角分别为C红=60°,C紫=45°,
而光线在AB面上入射角i=45°,说明紫光恰好发生了全反射,红光从AB面有反射,也有折射.所以在AM区域的亮斑P1为红色,
在AN区域的亮斑P2为红色与紫色的混合色.
②画出如图光路图.
设折射角为r,两个光斑分别为P1、P2,根据折射定律得
n1=
| sinr |
| sini |
求得sinr=
| ||
| 3 |
由几何知识可得tanr=
| R |
| AP1 |
解得AP1=7.05×10-2m
由几何知识可得△OAP2为等腰直角三角形,
解得AP2=0.1m
所以P1P2=(5
| 2 |
答:①在AM区域的亮斑P1为红色,在AN区域的亮斑P2为红色与紫色的混合色.
②两个亮斑间的距离是0.17m.


练习册系列答案
相关题目