题目内容
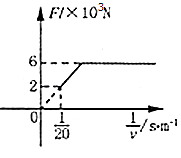
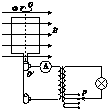
【题目】如图甲所示,两水平金属板间电场强度的变化规律如图乙所示.t=0时刻,质量为m的带电微粒以初速度V0沿中线射入两板间,0~ ![]() 时间内微粒匀速运动,T时刻微粒从金属板的右边飞出.微粒运动过程中未与金属板接触.重力加速度的大小为g,求:
时间内微粒匀速运动,T时刻微粒从金属板的右边飞出.微粒运动过程中未与金属板接触.重力加速度的大小为g,求:
(1)微粒飞出极板时速度的大小;
(2)整个过程中微粒重力势能变化量.
【答案】
(1)
解:由0~ ![]() 时间内微粒匀速运动,则有:qE0=mg.
时间内微粒匀速运动,则有:qE0=mg.
![]() ~
~ ![]() 内微粒只受到质量的作用,做平抛运动,竖直方向下降的位移 y1=
内微粒只受到质量的作用,做平抛运动,竖直方向下降的位移 y1= ![]() g(
g( ![]() )2=
)2= ![]()
在 ![]() ~T时间内微粒的加速度 a=
~T时间内微粒的加速度 a= ![]() =2g,方向竖直向上,微粒在竖直方向上做匀减速运动,
=2g,方向竖直向上,微粒在竖直方向上做匀减速运动,
微粒在水平方向做匀速直线运动,在竖直方向上选取向下为正方向,则: ![]()
微粒的末速度:v= ![]()
(2)
解:在 ![]() 时刻微粒在竖直方向的分速度:
时刻微粒在竖直方向的分速度: ![]()
在 ![]() ~T时间内,微粒竖直方向上的位移:
~T时间内,微粒竖直方向上的位移: ![]()
则微粒在0~T时间内在竖直方向的位移:y=y1+y2
则微粒重力势能减少:△EP=mgy
代入数据,联立得: ![]()
【解析】(1)0~ ![]() 时间内微粒匀速运动,重力和电场力相等,
时间内微粒匀速运动,重力和电场力相等, ![]() ~
~ ![]() 内,微粒做平抛运动,
内,微粒做平抛运动, ![]() ~T时间内,微粒竖直方向上做匀减速运动,水平方向上始终做匀速直线运动,结合牛顿第二定律和运动学公式进行求解.(2)重力势能的变化等于重力做的功,由此即可求出.
~T时间内,微粒竖直方向上做匀减速运动,水平方向上始终做匀速直线运动,结合牛顿第二定律和运动学公式进行求解.(2)重力势能的变化等于重力做的功,由此即可求出.
【考点精析】认真审题,首先需要了解匀变速直线运动的速度、位移、时间的关系(速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值).

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目