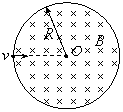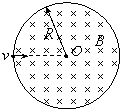题目内容
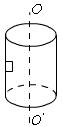
如图所示,半径为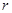 的圆筒,绕竖直中心轴
的圆筒,绕竖直中心轴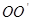 旋转,小物块
旋转,小物块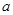 靠在圆筒的内壁上,它与圆筒内壁间的动摩擦因数为
靠在圆筒的内壁上,它与圆筒内壁间的动摩擦因数为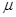 ,现要使
,现要使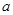 不下落,则圆筒转动的角速度
不下落,则圆筒转动的角速度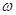 至少为( )
至少为( )
A.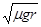 B.
B.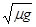 C.
C.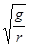 D.
D.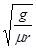
【答案】
D
【解析】
试题分析:筒壁对物体的静摩擦力与重力相平衡,筒壁对物体的支持力提供向心力,根据向心力公式即可求解.
要使A不下落,则小物块在竖直方向上受力平衡,有:f=mg
当摩擦力正好等于滑动摩擦力时,圆筒转动的角速度ω取最小值,筒壁对物体的支持力提供向心力,
根据向心力公式得;
N=mω2r
而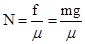 解得:
解得: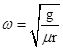
故选:D。
考点:向心力;牛顿第二定律.
点评:物体在圆筒内壁做匀速圆周运动,向心力是由筒壁对物体的支持力提供的.而物体放在圆盘上随着圆盘做匀速圆周运动时,此时的向心力是由圆盘的静摩擦力提供的.

练习册系列答案
相关题目
 如图所示,半径为r,质量不计的圆盘盘面与地面相垂直,圆心处有一个垂直盘面的光滑水平固定轴O,在盘的最右边缘固定一个质量为m的小球A,在O点的正下方离O点r/2处固定一个质量也为m的小球B.放开盘让其自由转动,问:
如图所示,半径为r,质量不计的圆盘盘面与地面相垂直,圆心处有一个垂直盘面的光滑水平固定轴O,在盘的最右边缘固定一个质量为m的小球A,在O点的正下方离O点r/2处固定一个质量也为m的小球B.放开盘让其自由转动,问:
 如图所示,半径为r,质量不计的圆盘与地面垂直,圆心处有一个垂直盘面的光滑水平固定轴O,在盘的最右边缘固定一个质量为m的小球A,在O点的正下方离O点r/2处固定一个质量也为m的小球B.放开盘让其自由转动,问:
如图所示,半径为r,质量不计的圆盘与地面垂直,圆心处有一个垂直盘面的光滑水平固定轴O,在盘的最右边缘固定一个质量为m的小球A,在O点的正下方离O点r/2处固定一个质量也为m的小球B.放开盘让其自由转动,问: