题目内容
(1)静止的原子核
U处在一个匀强磁场中,当它自发地放出一个α粒子后变成一个新核.若α粒子放出时的速度方向与磁感应强度方向垂直,则α粒子与新核做匀速圆周运动的轨道半径之比为 从α粒子放出到它与新生核相遇的过程中,α粒子至少转 圈.
(2)已知氮核的质量为14.00735u,氧核的质量为17.00454u,氦核的质量为4.00387u,质子的质量为1.00815u,则核反应
N+
He→
O+
H是 (填“释能”“吸能”)反应,能量变化了 J(1u相当于931MeV).
238 92 |
(2)已知氮核的质量为14.00735u,氧核的质量为17.00454u,氦核的质量为4.00387u,质子的质量为1.00815u,则核反应
14 7 |
4 2 |
17 8 |
1 1 |
分析:(1)原子核衰变过程动量守恒,衰变新核与α粒子都做圆周运动,由牛顿第二定律求出轨道半径,然后求出半径之比,求出新核与粒子的周期,然后根据新核与α粒的周期分析答题.
(2)通过反应前后质量的变化,即可判断吸能还是放能,然后根据质能方程求出能量的大小.
(2)通过反应前后质量的变化,即可判断吸能还是放能,然后根据质能方程求出能量的大小.
解答:解:(1)原子核衰变时动量守恒,由动量守恒定律可知,新核与α粒子的动量p大小相等,
它们在磁场中做匀速圆周运动,由牛顿第二定律可得:qvB=m
,轨道半径r=
=
,
它们的轨道半径之比:
=
=
=
=
;
做圆周运动的周期T=
,则它们的周期之比:
=
=
=
×
=
,
它们再次相遇时,运动时间相等,α粒子需要转13圈,新核需要转10圈;
(2)根据题意反应前的质量为:m1=14.00735u+4.00387u=18.01122u,
反应后:m2=17.00454u+1.00815u=18.01269u,
m2>m1因此质量增量了,故是吸能反应.
根据质能方程有:△E=△mc2=(18.01269-18.01122)×931.MeV=1.36857Mev≈2.2×10-13J;
故答案为:(1)45:1;13;(2)吸能; 2.2×10-13.
它们在磁场中做匀速圆周运动,由牛顿第二定律可得:qvB=m
| v2 |
| r |
| mv |
| qB |
| p |
| qB |
它们的轨道半径之比:
| rα |
| r新核 |
| ||
|
| q新核 |
| qα |
| 92-2 |
| 2 |
| 45 |
| 1 |
做圆周运动的周期T=
| 2πm |
| qB |
| Tα |
| T新核 |
| ||
|
| mαq新核 |
| m新核qα |
| 4 |
| 238-4 |
| 92-2 |
| 2 |
| 10 |
| 13 |
它们再次相遇时,运动时间相等,α粒子需要转13圈,新核需要转10圈;
(2)根据题意反应前的质量为:m1=14.00735u+4.00387u=18.01122u,
反应后:m2=17.00454u+1.00815u=18.01269u,
m2>m1因此质量增量了,故是吸能反应.
根据质能方程有:△E=△mc2=(18.01269-18.01122)×931.MeV=1.36857Mev≈2.2×10-13J;
故答案为:(1)45:1;13;(2)吸能; 2.2×10-13.
点评:(1)本题比较简单考查了粒子的圆周运动、动量守恒,题目难度不大,应牢牢固掌握基础知识,灵活应用基础知识是即可正确解题.
(2)本题考查了核反应前后的质量变化以及质能方程的应用,属于简单基础题目.
(2)本题考查了核反应前后的质量变化以及质能方程的应用,属于简单基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
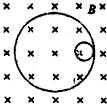 一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16,则以下说法正确的是( )
一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16,则以下说法正确的是( )| A、该原子核发生了α衰变 | B、反冲核沿小圆做逆时针方向运动 | C、原静止的原子核的原子序数为17 | D、沿大圆和沿小圆运动的粒子的周期相同 |
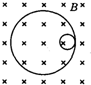 一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16( )
一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16( )