题目内容
（2005?河东区二模）原来静止的原子核
X，质量为m1，处在足够大的匀强磁场中，经α衰变变成质量为m2的原子核Y，α粒子的质量是m3，已测得α粒子的速度垂直磁场B，且动能为E0．假定原子核X衰变时释放的核能全部转化为动能，则下列结论正确的是 （ ）
（1）核Y与α粒子在磁场中运动周期之比为
（2）核Y与α粒子在磁场中运动的半径之比为
（3）此衰变过程中的质量亏损为m1-m2-m3
（4）此衰变过程中释放的核能为
．
A Z |
（1）核Y与α粒子在磁场中运动周期之比为
| z |
| z-2 |
（2）核Y与α粒子在磁场中运动的半径之比为
| 2 |
| z-2 |
（3）此衰变过程中的质量亏损为m1-m2-m3
（4）此衰变过程中释放的核能为
| AE0 |
| A-4 |
分析：α粒子的符号是
He，根据电荷数守恒和质量数守恒书写核衰变反应方程，衰变过程遵守动量守恒和能量守恒．由磁场中圆周运动半径公式r=
和周期公式T=
，分析半径和周期关系．根据能量守恒和动量守恒求解核衰变反应中释放出的核能．
4 2 |
| mv |
| qB |
| 2πm |
| qB |
解答：解：根据电荷数守恒和质量数守恒，核衰变反应方程为：
X→
He+
Y
（1）根据周期公式T=
，得周期之比为
=
：
=
?
．故（1）错误．
（2）根据半径公式r=
，又mv=P（动量），则得r=
①
在衰变过程遵守动量守恒，根据动量守恒定律得：0=PY-Pα，则PY=Pα，②
由①②得：半径之比为
=
=
．故（2）正确．
（3）发生衰变时的质量亏损为△m=m1-m2-m3．故（3）正确．
（4）由动能与动量的关系：Ek=
，得原子核Y与α粒子的动能之比为：
=
=
，则得EkY=
E0
由题，原子核X衰变时释放的核能全部转化为动能，则有释放的核能为E=Ekα+EkY=
．故（4）正确．
故选B
A Z |
4 2 |
A-4 Z-2 |
（1）根据周期公式T=
| 2πm |
| qB |
| TY |
| Tα |
| mY |
| qY |
| mα |
| qα |
| A-4 |
| 4 |
| 2 |
| Z-2 |
（2）根据半径公式r=
| mv |
| qB |
| P |
| qB |
在衰变过程遵守动量守恒，根据动量守恒定律得：0=PY-Pα，则PY=Pα，②
由①②得：半径之比为
| rY |
| rα |
| qα |
| qY |
| 2 |
| Z-2 |
（3）发生衰变时的质量亏损为△m=m1-m2-m3．故（3）正确．
（4）由动能与动量的关系：Ek=
| P2 |
| 2m |
| EkY |
| Ekα |
| mα |
| mY |
| 4 |
| A-4 |
| 4 |
| A-4 |
由题，原子核X衰变时释放的核能全部转化为动能，则有释放的核能为E=Ekα+EkY=
| AE0 |
| A-4 |
故选B
点评：核反应遵守的基本规律有动量守恒和能量守恒，书写核反应方程式要遵循电荷数守恒和质量数守恒．结合磁场的知识即可分析．
练习册系列答案
相关题目
（2005?河东区二模）1931年英国物理学家狄拉克从理论上预言，存在只有一个磁极的粒子，即“磁单极子”．1982年英国物理学家卡布莱设计了一个寻找磁单极子的实验，他设想，如果一个只有N极的磁单极子从上向下穿过一个如图所示的超导线圈，那么从上向下看，超导线圈上将出现 （ ）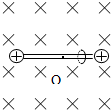
（2005?河东区二模）如图所示，两个等量的正电荷Q1、Q2固定在绝缘光滑水平面上，两点电荷用一光滑绝缘杆相连，O点为杆的中点，杆上有一带正电的小环，杆所在的区域存在一个沿水平方向且与杆垂直的匀强磁场，将小环由静止从图示位置开始释放，在小环运动过程中，下列说法中正确的是：（ ）