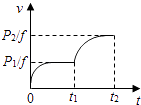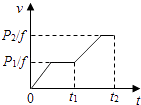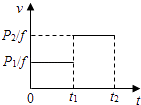题目内容
【题目】如图所示，CD左侧存在场强大小E= 
，方向水平向左的匀强电场，一个质量为m、电荷量为+q的光滑绝缘小球，从底边BC长为L、倾角53°的光滑直角三角形斜面顶端A点由静止开始下滑，运动到斜面底端C点后进入一光滑竖直半圆形细圆管内（C处为一小段长度可忽略的光滑圆弧，圆管内径略大于小球直径，半圆直径CD在竖直线上），恰能到达细圆管最高点D点，随后从D点离开后落回斜面上某点P．（重力加速度为g，sin53°=0.8，Cos53°=0.6）求：
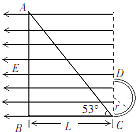
（1）小球到达C点时的速度；
（2）小球从D点运动到P点的时间t．
【答案】
（1）
解：由动能定理：
mg 
L﹣qEL= 
mv2 …①
解得：v= 
…②
（2）
解：由A到D的过程由动能定理：
mg 
L﹣mg2r﹣qEL=0 …③
得：r= 
…④
离开D点后做匀加速直线运动，如图．
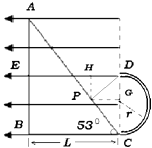
竖直方向：SDG= gt2 …⑤
水平方向：qE=ma …⑥
SDH= at2…⑦
又由几何关系得：
…⑧
解得：t= 
…⑨
【解析】（1）由动能定理即可求得速度（2）利用动能定理求的轨道半径，利用水平方向和竖直方向的运动即可求得时间
【考点精析】认真审题，首先需要了解动能定理的综合应用(应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷)．
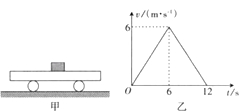
【题目】验证机械能守恒定律的方法很多，落体法验证机械能守恒定律就是其中的一种，图示是利用透明直尺自由下落和光电计时器来验证机械能守恒定律的简易示意图．当有不透光的物体从光电门间通过时，光电计时器就可以显示物体的挡光时间，所用的光电门传感器可测得最短时间为0.01ms．将挡光效果好、宽度d=3.8×10﹣3m的黑色磁带贴在透明直尺上，现将直尺从一定高度由静止释放，并使其竖直通过光电门．一同学测得各段黑色磁带通过光电门的时间△ti与图中所示的高度差△hi ， 并将部分数据进行了处理，结果如图所示．（取g=9.8m/s2 ， 表格中M=0.1kg为直尺的质量）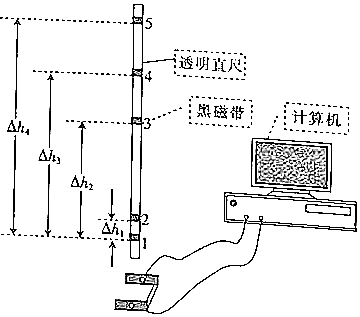
△ti（×10﹣3s） | vi= | △Eki= | △hi（m） | Mghi（J） | |
1 | 1.21 | 3.14 | ﹣ | ﹣ | ﹣ |
2 | 1.15 | 3.30 | 0.052 | 0.06 | 0.059 |
3 | 1.00 | 3.80 | 0.229 | 0.24 | 0.235 |
4 | 0.95 | 4.00 | 0.307 | 0.32 | 0.314 |
5 | 0.90 | ① | ② | 0.41 | ③ |
（1）从表格中的数据可知，直尺上磁带通过光电门的瞬时速度是利用vi= 
求出的，请你简要分析该同学这样做的理由是： ．
（2）表格中的数据①、②、③分别为、、 ．
（3）通过实验得出的结论是： ．
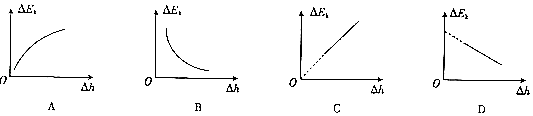
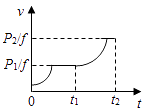
（4）根据该实验，请你判断下列△Ek﹣△h图象中正确的是 ． 
