Question

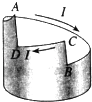
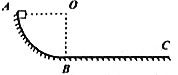
【题目】如图所示，在竖直平面内有一条不光滑的轨道ABC，其中AB段是半径为R的圆弧，BC段是水平的。一质量为m的滑块从A点由静止滑下，最后停在水平轨道上C点，此过程克服摩擦力做功为W1。现用一沿着轨道方向的力推滑块，使它缓慢地由C点推回到A点，此过程克服摩擦力做功为W2，设推力对滑块做功为W，则下列关系中正确的是

A. W1=mgR B. W2= mgR

C. mgR< W<2mgR D. W> 2mgR

Answer 1

【答案】AC

【解析】

由于运动形式不同，所以从A到B与从B到A克服摩擦力做功也不相同，在做此题时要注意这个特征。

A、滑块由A到C的过程，由动能定理可知 ,故A对；

B、滑块由A到B做圆周运动，而在推力作用下从C经过B到达A的过程是一个匀速过程，所以从A到B的过程中平均支持力大于从B到A 的平均支持力，那么摩擦力做功即为从A到B的功大于从B到A的功，即 ，故B错；

CD、滑块由C到A的过程中,由能量守恒可知，推力对滑块做功等于滑块重力势能增加量与克服摩擦所做功两部分，即 即，由于 ，所以mgR< W<2mgR，故C对，D错；

故选AC