��Ŀ����
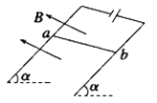
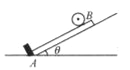
����Ŀ����ͼ��ʾ�����Ϊ30���Ĺ⻬б����¶���һˮƽ���ʹ������ʹ�����6m/s���ٶ��˶����˶�������ͼ��ʾ��һ������Ϊ2kg�����壨���������Ϊ�ʵ㣩����h=3.2m�ߴ��ɾ�ֹ��б���»������徭��A��ʱ�������Ǵ�б�浽���ʹ����ǴӴ��ʹ���б�棬�������䶯����ʧ�������봫�ʹ���Ķ�Ħ������Ϊ0.5���������ٶ�g=10m/s2����

��1�������һ�ε���A��ʱ�ٶ�Ϊ���
��2��Ҫʹ���岻�Ӵ��ʹ��ϻ��䣬���ʹ�AB��ľ������ٶ��
��3�������洫�ʹ������˶��������б���ϻ������߶�Ϊ���٣�
���𰸡���1��8m/s ��2��6.4m ��3��1.8m
��������
��1�������������ɹ⻬б���»��Ĺ��̣�ֻ���������������ݻ�е���غ�������嵽б��ĩ�˵��ٶȴ�С��
��2�������廬�����ʹ�������ٶ�Ϊ��ʱ��AB��ľ���L��С�����ݶ��ܶ�����ʽ��⣻
��3�������ڵ���A��ǰ�ٶ��봫�ʹ���ȣ������6m/s���ٶȳ���б��ʱ��б���ϻ��ﵽ�ĸ߶�����ݶ��ܶ�����⼴�ɡ�
��1�������ɹ⻬б���»��Ĺ����У�ֻ��������������е���غ㣬��ã�![]()
��ã�![]()
��2�������廬�������ʹ�������ٶ�Ϊ��ʱ��AB��ľ���L��С���ɶ��������ã�![]()
��ã�![]()
��3����Ϊ���ϴ��ʹ����ٶ���8m/s���ڴ��ʹ����ٶ�6m/s�������ڵ���A��ǰ�ٶ��봫�ʹ���ȣ������![]() ���ٶȳ���б�棬���ݶ��ܶ����ã�
���ٶȳ���б�棬���ݶ��ܶ����ã�![]()
�ã�![]()