题目内容
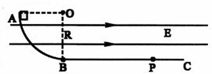 (2009?天津模拟)如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)
(2009?天津模拟)如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)(1)求滑块到达B点前瞬间对轨道的压力大小.
(2)求BP间的距离.
分析:(1)根据动能定理求出滑块滑到B点时的速度,再根据牛顿第二定律求出滑块对轨道的压力.
(2)对BP段运用动能定理,抓住电场力和摩擦力做功求出BP间的距离.
(2)对BP段运用动能定理,抓住电场力和摩擦力做功求出BP间的距离.
解答:解:(1)A到B的过程由动能定理得,
-qER+mgR=
mvB2-0
解得vB=3m/s.
在B处,由牛顿第二定律得,NB-mg=m
解得NB=28N.
根据牛顿第三定律,小球对轨道的压力NB′=NB=28N.
(2)设BP间的距离为s,对BP过程运用动能定理得,
-qEs+(-μmgs)=0-
mvB2
解得s=1.5m.
答:(1)滑块到达B点前瞬间对轨道的压力大小为28N.
(2)BP间的距离为1.5m.
-qER+mgR=
| 1 |
| 2 |
解得vB=3m/s.
在B处,由牛顿第二定律得,NB-mg=m
| vB2 |
| R |
解得NB=28N.
根据牛顿第三定律,小球对轨道的压力NB′=NB=28N.
(2)设BP间的距离为s,对BP过程运用动能定理得,
-qEs+(-μmgs)=0-
| 1 |
| 2 |
解得s=1.5m.
答:(1)滑块到达B点前瞬间对轨道的压力大小为28N.
(2)BP间的距离为1.5m.
点评:本题综合考查了动能定理和牛顿第二定律,难度不大,关键搞清滑块通过B点时向心力的来源.

练习册系列答案
相关题目
 (2009?天津模拟)振源A带动细绳上下振动,某时刻在绳上形成的横波波形如图甲所示,规定绳上各质点向上运动的方向为位移x的正方向,从波传播到细绳上的P点开始计时,下列图乙的四个图形中能表示P点振动图象的是( )
(2009?天津模拟)振源A带动细绳上下振动,某时刻在绳上形成的横波波形如图甲所示,规定绳上各质点向上运动的方向为位移x的正方向,从波传播到细绳上的P点开始计时,下列图乙的四个图形中能表示P点振动图象的是( ) (2009?天津模拟)在如图所示的电路中,灯泡L的电阻大于电源的内阻r,闭合电键S,将滑动变阻器滑片P向左移动一段距离后,下列结论正确的是( )
(2009?天津模拟)在如图所示的电路中,灯泡L的电阻大于电源的内阻r,闭合电键S,将滑动变阻器滑片P向左移动一段距离后,下列结论正确的是( )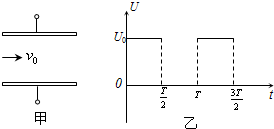 (2009?天津模拟)在如图甲所示的两平行金属板上加有如图乙所示的电压,该电压的周期为T,大量电子(其重力不计)以相同的初速度连续不断地沿平行于金属板的方向从两板间射入电场,并都能从两板间通过,且飞行时间为T,不考虑电子间的相互作用力,下列说法正确的是( )
(2009?天津模拟)在如图甲所示的两平行金属板上加有如图乙所示的电压,该电压的周期为T,大量电子(其重力不计)以相同的初速度连续不断地沿平行于金属板的方向从两板间射入电场,并都能从两板间通过,且飞行时间为T,不考虑电子间的相互作用力,下列说法正确的是( )