题目内容
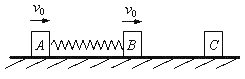
【题目】质量为M=2kg的小平板车静止在光滑水平面上,车的一端静止着质量为mA=2kg的物体A(可视为质点),如图所示,一颗质量为mB=20g的子弹以600m/s的水平速度射穿A后,速度变为100m/s,最后物体A仍静止在车上,若物体A与小车间的动摩擦因数μ=0.5,取g=10m/s2,求

(1)平板车最后的速度是多大?
(2)小车长度至少是多少.
【答案】(1) ![]() (2)
(2)![]()
【解析】子弹击中物体过程中,系统动量守恒,以子弹的初速度方向为正方向,由动量守恒定律得:
mBv0=mBv′+mAvA,
0.02×600=0.02×100+2vA,
解得:vA=5m/s,
平板车与物体A组成的系统自子弹穿出后直至相对静止过程中系统动量守恒,以A的初速度方向为正方向,由动量守恒定律得:mAvA=(M+mA)v车,代入数据解得,平板车最后速度为:v车=![]() =2.5m/s;
=2.5m/s;
物体和平板车损失的机械能全转化为系统发热,假设A在平板车上滑行距离为s,由能量守恒定律得:μmAgs=![]() mAvA2-
mAvA2-![]() (M+mA)v车2,
(M+mA)v车2,
即:0.5×2×10s=![]() ×2×52-
×2×52-![]() ×(2+2)×2.52,
×(2+2)×2.52,
解得:s=1.25m,

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目