题目内容
 如图所示,物体从A点由静止开始做匀加速直线运动,到达B点后,在外力作用下做匀减速直线运动到C点恰好停下.用速度传感器测量物体的瞬时速度,下表给出了部分测量数据.
如图所示,物体从A点由静止开始做匀加速直线运动,到达B点后,在外力作用下做匀减速直线运动到C点恰好停下.用速度传感器测量物体的瞬时速度,下表给出了部分测量数据.| t(s) | 0.0 | 0.2 | 0.4 | … | 2.4 | 2.6 | … |
| v(m/s) | 0.0 | 0.4 | 0.8 | … | 2.0 | 1.0 | … |
(1)在AB段的加速度a1、BC段加速度a2
(2)AB段和BC段长度之比
(3)t=2.1s时的瞬时速度v 大小.
分析:(1)由加速度的定义式可解得两个过程的加速度;
(2)根据运动学速度位移关系公式求解加速过程和减速过程位移之比,即AB段和BC段长度之比.
(3)瞬时速度则可以用速度时间关系式求解.
(2)根据运动学速度位移关系公式求解加速过程和减速过程位移之比,即AB段和BC段长度之比.
(3)瞬时速度则可以用速度时间关系式求解.
解答:解:(1)在AB段的加速度a1=
=
=2m/s2
BC段加速度a2=
=-5m/s2
(2)设物体经过B点速度为v,则
v2=2xABa1
0-v2=2xBCa2
则得:
=-
=
(3)设加速过程的时间为t,则从t时刻到2.4s列速度时间关系式:
v′=v+a2(2.4-t)
又v=a1t
代入得:2=v-5(2.4-t)
v=2t
解得:t=2s; v=4m/s
t=2.1s时的瞬时速度v″=v+a2(2.1-t)=4-5×(2.1-2)=3.5m/s
答:
(1)在AB段的加速度a1、BC段加速度a2分别为2m/s2 和-5m/s2.
(2)AB段和BC段长度之比是5:2.
(3)t=2.1s时的瞬时速度v 大小是3.5m/s.
| △v |
| △t |
| 0.8-0.4 |
| 0.2 |
BC段加速度a2=
| 1-2 |
| 0.2 |
(2)设物体经过B点速度为v,则
v2=2xABa1
0-v2=2xBCa2
则得:
| xAB |
| xBC |
| a2 |
| a1 |
| 5 |
| 2 |
(3)设加速过程的时间为t,则从t时刻到2.4s列速度时间关系式:
v′=v+a2(2.4-t)
又v=a1t
代入得:2=v-5(2.4-t)
v=2t
解得:t=2s; v=4m/s
t=2.1s时的瞬时速度v″=v+a2(2.1-t)=4-5×(2.1-2)=3.5m/s
答:
(1)在AB段的加速度a1、BC段加速度a2分别为2m/s2 和-5m/s2.
(2)AB段和BC段长度之比是5:2.
(3)t=2.1s时的瞬时速度v 大小是3.5m/s.
点评:在高中物理学习中,我们会遇到多种不同的获取信息方法,这些方法对我们理解物理有很大的帮助.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
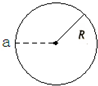 如图所示,物体从a点出发沿半径为R的圆弧运动一周,则下列说法正确的是( )
如图所示,物体从a点出发沿半径为R的圆弧运动一周,则下列说法正确的是( )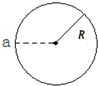 如图所示,物体从a点出发沿半径为R的圆弧运动一周,则下列说法正确的是
如图所示,物体从a点出发沿半径为R的圆弧运动一周,则下列说法正确的是