题目内容
 如图所示,带有倾角为θ的斜面的质量为M的楔形物体B放在水平面上,质量为m的物块A放在其斜面上,A在水平推力F的作用下沿斜面以加速度a匀加速上升,此过程中B保持静止状态,则据此不能求出的物理量是
如图所示,带有倾角为θ的斜面的质量为M的楔形物体B放在水平面上,质量为m的物块A放在其斜面上,A在水平推力F的作用下沿斜面以加速度a匀加速上升,此过程中B保持静止状态,则据此不能求出的物理量是
- A.A、B之间的动摩擦因数
- B.物体B与地面之间的动摩擦因数
- C.物体B在此过程中所受地面的摩擦力
- D.物体B在此过程中所受地面的支持力
B
分析:先对滑块受力分析,受重力、推力、支持力和摩擦力,根据牛顿第二定律列式求解;再对AB整体受力分析并根据牛顿第二定律列式求解.
解答:A、对滑块受力分析,受重力、推力、支持力和摩擦力;
滑块匀加速上滑,加速度为a,根据牛顿第二定律,有
平行斜面方向:Fcosθ-mgsinθ-μ(Fsinθ+mgcosθ)=ma
可以求解出动摩擦因素,故A错误;
B、C、D、对AB整体受力分析,受总重力、支持力、推力、向左的静摩擦力,根据牛顿第二定律,有
水平方向:F-f静=macosθ
竖直方向:N-(M+m)g=masinθ
解得f静=macosθ+F,故C错误;
解得N=(M+m)g+masinθ,故D错误;
由于滑动摩擦力未知,故无法求解斜面体与地面间的动摩擦因素,故B正确;
故选B.
点评:本题关键灵活地选择研究对象,受力分析后根据牛顿第二定律列式求解;对于整体,是加速度不同的连接体,较难.
分析:先对滑块受力分析,受重力、推力、支持力和摩擦力,根据牛顿第二定律列式求解;再对AB整体受力分析并根据牛顿第二定律列式求解.
解答:A、对滑块受力分析,受重力、推力、支持力和摩擦力;
滑块匀加速上滑,加速度为a,根据牛顿第二定律,有
平行斜面方向:Fcosθ-mgsinθ-μ(Fsinθ+mgcosθ)=ma
可以求解出动摩擦因素,故A错误;
B、C、D、对AB整体受力分析,受总重力、支持力、推力、向左的静摩擦力,根据牛顿第二定律,有
水平方向:F-f静=macosθ
竖直方向:N-(M+m)g=masinθ
解得f静=macosθ+F,故C错误;
解得N=(M+m)g+masinθ,故D错误;
由于滑动摩擦力未知,故无法求解斜面体与地面间的动摩擦因素,故B正确;
故选B.
点评:本题关键灵活地选择研究对象,受力分析后根据牛顿第二定律列式求解;对于整体,是加速度不同的连接体,较难.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 如图所示,带有倾角为θ的斜面的质量为M的楔形物体B放在水平面上,质量为m的物块A放在其斜面上,A在水平推力F的作用下沿斜面以加速度a匀加速上升,此过程中B保持静止状态,则据此不能求出的物理量是( )
如图所示,带有倾角为θ的斜面的质量为M的楔形物体B放在水平面上,质量为m的物块A放在其斜面上,A在水平推力F的作用下沿斜面以加速度a匀加速上升,此过程中B保持静止状态,则据此不能求出的物理量是( )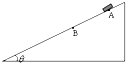 (2012?武昌区模拟)如图所示,斜面倾角为θ,斜面上AB段光滑,其它部分粗糙,且斜面足够长.一带有速度传感器的小物块(可视为质点),自A点由静止开始沿斜面下滑,速度传感器上显示的速度与运动时间的关系如下表所示:
(2012?武昌区模拟)如图所示,斜面倾角为θ,斜面上AB段光滑,其它部分粗糙,且斜面足够长.一带有速度传感器的小物块(可视为质点),自A点由静止开始沿斜面下滑,速度传感器上显示的速度与运动时间的关系如下表所示:
