题目内容
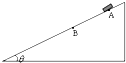 (2012?武昌区模拟)如图所示,斜面倾角为θ,斜面上AB段光滑,其它部分粗糙,且斜面足够长.一带有速度传感器的小物块(可视为质点),自A点由静止开始沿斜面下滑,速度传感器上显示的速度与运动时间的关系如下表所示:
(2012?武昌区模拟)如图所示,斜面倾角为θ,斜面上AB段光滑,其它部分粗糙,且斜面足够长.一带有速度传感器的小物块(可视为质点),自A点由静止开始沿斜面下滑,速度传感器上显示的速度与运动时间的关系如下表所示:| 时间(s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | …. |
| 速度(m/s) | 0 | 6 | 12 | 17 | 21 | 25 | 29 | … |
(1)斜面的倾角θ多大?
(2)小物块与斜面的粗糙部分间的动摩擦因数μ为多少?
(3)AB间的距离xAB等于多少?
分析:(1)光滑段物体受重力和支持力,由表格数据得到物体在光滑段的加速度,然后根据牛顿第二定律列式求解斜面的倾角θ;
(2)粗糙段物体受重力、支持力和滑动摩擦力,根据表格数据得到物体该段的加速度,然后结合牛顿第二定律列式求解动摩擦因素;
(3)根据速度时间关系公式列式求解AB段运动的时间,然后根据位移时间关系公式列式求解AB段的间距.
(2)粗糙段物体受重力、支持力和滑动摩擦力,根据表格数据得到物体该段的加速度,然后结合牛顿第二定律列式求解动摩擦因素;
(3)根据速度时间关系公式列式求解AB段运动的时间,然后根据位移时间关系公式列式求解AB段的间距.
解答:解:(1)当小物块在AB段运动时,设加速度为a1,则 a1=
=gsinθ
由表格可知:a1=
m/s2=6m/s2
所以 θ=370
(2)过B点后物块的加速度设为a2,则a2=gsinθ-μgcosθ
由表格可知 a2=
m/s2=4m/s2
所以 μ=0.25
(3)可以判断B点对应于2s~3s之间的某个时刻,设t1为从第2s时刻运动至B点所用时间,t2为从B点运动至第3s时刻所用时间.
则t1+t2=1s
根据速度时间关系公式,有:12m/s+a1t1=17m/s-a2t2
解之得 t1=0.5s
所以 xAB=
a1(2+t1)2=
×6×(2+0.5)2=18.75m
答:(1)斜面的倾角θ为37°;
(2)小物块与斜面的粗糙部分间的动摩擦因数μ为为0.25;
(3)AB间的距离xAB等于18.75m.
| F合 |
| m |
由表格可知:a1=
| 12-0 |
| 2-0 |
所以 θ=370
(2)过B点后物块的加速度设为a2,则a2=gsinθ-μgcosθ
由表格可知 a2=
| 29-21 |
| 6-4 |
所以 μ=0.25
(3)可以判断B点对应于2s~3s之间的某个时刻,设t1为从第2s时刻运动至B点所用时间,t2为从B点运动至第3s时刻所用时间.
则t1+t2=1s
根据速度时间关系公式,有:12m/s+a1t1=17m/s-a2t2
解之得 t1=0.5s
所以 xAB=
| 1 |
| 2 |
| 1 |
| 2 |
答:(1)斜面的倾角θ为37°;
(2)小物块与斜面的粗糙部分间的动摩擦因数μ为为0.25;
(3)AB间的距离xAB等于18.75m.
点评:本题关键是明确滑块的运动规律,然后根据速度时间关系公式求解加速时间,根据位移时间关系公式求解位移,同时要结合牛顿第二定律判断受力情况.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
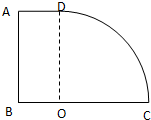 (2012?武昌区模拟)如图所示为用某种透明材料制成的一块柱形棱镜的截面图,圆弧CD为半径为R的四分之一的圆周,圆心为O,光线从AB面上的某点入射,入射角θ1=45°,它进入棱镜后恰好以临界角射在BC面上的O点.
(2012?武昌区模拟)如图所示为用某种透明材料制成的一块柱形棱镜的截面图,圆弧CD为半径为R的四分之一的圆周,圆心为O,光线从AB面上的某点入射,入射角θ1=45°,它进入棱镜后恰好以临界角射在BC面上的O点.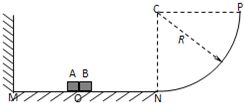 (2012?武昌区模拟)如图所示,质量均为m、可视为质点的A、B两物体紧挨着放在水平面上的O点,左边有竖直墙壁M,右边在P点与光滑的、半径为R的
(2012?武昌区模拟)如图所示,质量均为m、可视为质点的A、B两物体紧挨着放在水平面上的O点,左边有竖直墙壁M,右边在P点与光滑的、半径为R的