题目内容
2.在平直公路上有甲、乙两辆车在同一地点向同一方向运动,甲车以8m/s的速度做匀速直线运动,乙车从静止开始以2.0m/s的加速度作匀加速直线运动,问:(1)甲乙出发后,经多长时间再次相遇?
(2)在再次相遇前两车何时相距最远?最远距离是多少?
分析 (1)根据匀变速直线运动的位移公式,结合位移关系求出再次相遇的时间.
(2)当两车速度相等时,相距最远,结合速度公式和位移公式求出最远距离.
解答 解:(1)设经过t时间再次相遇,有:${v}_{甲}t=\frac{1}{2}a{t}^{2}$,代入数据解得t=$\frac{2{v}_{甲}}{a}=\frac{2×8}{2}s=8s$.
(2)当两车速度相等时,相距最远,即$t=\frac{{v}_{甲}}{a}=\frac{8}{2}s=4s$,
相距的最远距离$△x={v}_{甲}t-\frac{1}{2}a{t}^{2}$=$8×4-\frac{1}{2}×2×16m$=16m.
答:(1)甲乙出发后,经过8s时间再次相遇.
(2)再次相遇前两车经过4s相距最远,最远距离为16m.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式灵活求解,知道速度相等时,有最远距离.

练习册系列答案
相关题目
13.从地面竖直上抛物体A,同时在某一高度有一物体B自由下落,两物体在空中相遇时(并不相碰)速度大小都是v,则下列叙述错误的是( )
| A. | 物体的上抛速度是2v | |
| B. | 物体A和B的落地速度不同 | |
| C. | 物体A上升的最大高度和物体B开始下落的高度相同 | |
| D. | 物体A和B在空中运动的时间不同 |
11.下列运动中的物体不能看作质点的是( )
| A. | 航行的万吨巨轮在航海图上的位置 | B. | 研究大型客车在平直公路上的运动 | ||
| C. | 研究月球绕地球的转动 | D. | 研究电风扇通电后的转动 |
 在水平地面上有一个质量为4kg的物体,物体在水平拉力F的作用下由静止开始运动.10s末拉力减为$\frac{1}{3}$F,方向不变,该物体的v-t图象如图所示.求:
在水平地面上有一个质量为4kg的物体,物体在水平拉力F的作用下由静止开始运动.10s末拉力减为$\frac{1}{3}$F,方向不变,该物体的v-t图象如图所示.求: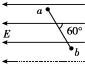 如图所示,在E=500V/m的匀强电场中,a、b两点相距d=2cm,它们的连线跟电场方向夹角是60°,则Uab=-5V.
如图所示,在E=500V/m的匀强电场中,a、b两点相距d=2cm,它们的连线跟电场方向夹角是60°,则Uab=-5V.