题目内容
18. 如图所示,一质量为m=1kg的小滑块,在F=6N水平拉力的作用下,从水平面上的A处由静止开始运动,滑行x=3m后由B处滑上倾角为37°的光滑斜面,滑上斜面后拉力的大小保持不变,方向变为沿斜面向上,滑动一段时间后撤去拉力.已知小滑块沿斜面上滑到的最远点C距B点为L=2.5m,小滑块最后恰好停在A处.不计B处能量损失,g取10m/s2,已知sin37°=0.6,cos37°=0.8.试求:
如图所示,一质量为m=1kg的小滑块,在F=6N水平拉力的作用下,从水平面上的A处由静止开始运动,滑行x=3m后由B处滑上倾角为37°的光滑斜面,滑上斜面后拉力的大小保持不变,方向变为沿斜面向上,滑动一段时间后撤去拉力.已知小滑块沿斜面上滑到的最远点C距B点为L=2.5m,小滑块最后恰好停在A处.不计B处能量损失,g取10m/s2,已知sin37°=0.6,cos37°=0.8.试求:(1)小滑块与水平面间的动摩擦因数μ.
(2)小滑块在斜面上运动时,拉力作用的距离x0.
(3)小滑块在斜面上运动时,拉力作用的时间t0(可用根号表示).
分析 (1)滑块从C运动到A时,运用动能定理求动摩擦因数μ.
(2)滑块从A运动到C的过程,由动能定理列式求解拉力作用的距离x0.
(3)根据牛顿第二定律求出滑块在斜面上运动时的加速度,由位移公式求解时间.
解答 解:(1)滑块从C运动到A时,由动能定理得
mgLsin37°-μmgx=0
可得 μ=0.5
(2)滑块从A运动到C的过程,由动能定理得
F(x+x0)-μmgx-mgLsin37°=0
代入得:6×(3+x0)-0.5×10×3-10×2.5×sin37°=0
解得 x0=2m
(3)滑块在拉力作用下在斜面上运动时的加速度 a=$\frac{F-mgsin37°}{m}$=$\frac{6-10×sin37°}{1}$=0,说明木块匀速运动.
设木块运动到B点的速度为v.由动能定理得
Fx-μmgx=$\frac{1}{2}m{v}^{2}$
解得 v=$\sqrt{6}$m/s
故小滑块在斜面上运动时,拉力作用的时间 t0=$\frac{{x}_{0}}{v}$=$\frac{2}{\sqrt{6}}$=$\frac{\sqrt{6}}{3}$s
答:
(1)小滑块与水平面间的动摩擦因数μ是0.5.
(2)小滑块在斜面上运动时,拉力作用的距离x0为2m
(3)小滑块在斜面上运动时,拉力作用的时间t0为$\frac{\sqrt{6}}{3}$s.
点评 解决该题关键要根据滑块运动情况,依据动能定理,列方程解答.注意在求解总功时要先对物体进行受力分析,找出每一个力做功的情况再求解.

练习册系列答案
相关题目
6.下列说法正确的是( )
| A. | 电流通过导体的热功率与电流大小成正比 | |
| B. | 力对物体所做的功与力的作用时间成正比 | |
| C. | 电容器所带电荷量与两极间的电势差成正比 | |
| D. | 弹性限度内,弹簧的劲度系数与弹簧伸长量成正比 |
7.宇航员王亚平在“天宮1号”飞船内进行了我国首次太空授课,演示了一些完全失重状态下的物理现象.若飞船质量为m,距地面高度为h,地球质量为M,半径为R,引力常量为G,则飞船所在处的重力加速度大小为( )
| A. | 0 | B. | $\frac{GM}{{{{(R+h)}^2}}}$ | C. | $\frac{GMm}{{{{(R+h)}^2}}}$ | D. | $\frac{GM}{h^2}$ |
17.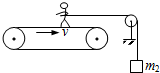 如图所示为一种测定运动员体能的装置,运动员的质量为m1,绳的一端拴在腰间并沿水平方向跨过滑轮(不计滑轮质量及摩擦),绳的下端悬挂一个质量为m2的重物,人用力蹬传送带而人的重心不动,使传送带以速率v匀速向右运动.下面说法中正确的是( )
如图所示为一种测定运动员体能的装置,运动员的质量为m1,绳的一端拴在腰间并沿水平方向跨过滑轮(不计滑轮质量及摩擦),绳的下端悬挂一个质量为m2的重物,人用力蹬传送带而人的重心不动,使传送带以速率v匀速向右运动.下面说法中正确的是( )
 如图所示为一种测定运动员体能的装置,运动员的质量为m1,绳的一端拴在腰间并沿水平方向跨过滑轮(不计滑轮质量及摩擦),绳的下端悬挂一个质量为m2的重物,人用力蹬传送带而人的重心不动,使传送带以速率v匀速向右运动.下面说法中正确的是( )
如图所示为一种测定运动员体能的装置,运动员的质量为m1,绳的一端拴在腰间并沿水平方向跨过滑轮(不计滑轮质量及摩擦),绳的下端悬挂一个质量为m2的重物,人用力蹬传送带而人的重心不动,使传送带以速率v匀速向右运动.下面说法中正确的是( )| A. | 绳子拉力对人做正功 | |
| B. | 人对传送带做正功 | |
| C. | 运动时间t后,运动员的体能消耗约为m1gvt | |
| D. | 运动时间t后,运动员的体能消耗约为(m1+m2)gvt |
 小明同学设计了一个“电磁天平”,如图1所示,等臂天平的左臂为挂盘,右臂挂有矩形线圈,两臂平衡,线圈的水平边长L=0.1m,竖直边长H=0.3m,匝数为N1,线圈的下边处于匀强磁场内,磁感应强度B0=1.0T,方向垂直线圈平面向里,线圈中通有可在0~2.0A范围内调节的电流I,挂盘放上待测物体后,调节线圈中电流使天平平衡,测出电流即可测得物体的质量(重力加速度取g=10m/s2)
小明同学设计了一个“电磁天平”,如图1所示,等臂天平的左臂为挂盘,右臂挂有矩形线圈,两臂平衡,线圈的水平边长L=0.1m,竖直边长H=0.3m,匝数为N1,线圈的下边处于匀强磁场内,磁感应强度B0=1.0T,方向垂直线圈平面向里,线圈中通有可在0~2.0A范围内调节的电流I,挂盘放上待测物体后,调节线圈中电流使天平平衡,测出电流即可测得物体的质量(重力加速度取g=10m/s2) 如图所示,一倾角为30°的光滑斜面固定在地面上,一质量为m的小木块在水平力F的作用下静止在斜面上,若只改变F的方向不改变F的大小,仍使木块静止,则此时力F与水平面的夹角为60°.
如图所示,一倾角为30°的光滑斜面固定在地面上,一质量为m的小木块在水平力F的作用下静止在斜面上,若只改变F的方向不改变F的大小,仍使木块静止,则此时力F与水平面的夹角为60°.