题目内容
半径r=0.4m的光滑绝缘轨道固定于竖直平面内，加上某一方向的匀强电场时，带电小球沿轨道内侧做圆周运动，小球动能最大的位置在A点，圆心O与A点的连线与竖直线成一角度如图所示，小球经过A点时，对轨道的压力为N=108N，若小球的最大动能比最小初动能多14.4J，且小球能够到达轨道上任意的一点，试求：
（1）小球的最小动能为多少？
（2）若小球在动能最小位置时突然撤去轨道，并保持其它条件不变，则小球经0.02s时，其动能与A点时的动能相等，小球的质量为多大？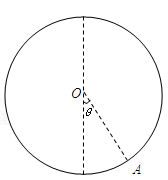
（1）小球的最小动能为多少？
（2）若小球在动能最小位置时突然撤去轨道，并保持其它条件不变，则小球经0.02s时，其动能与A点时的动能相等，小球的质量为多大？
(1)3.6J(2)4.5*10-3kg
据题分析可知，小球的重力与电场力的合力方向必沿OA连线向下，
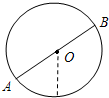
最小动能的位置必在A点关于O点对称的B点, 则有F?2R=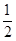
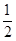mvA2-mvB2 代入解得F=18N
在A点时有 N-F=m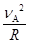
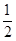mvA2=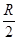
（N-F）=18J
所以最小动能为Ekm=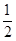mvB2=18J-14.4J=3.6J
②在B点撤去轨道后，小球将做类平抛运动: 由2R=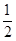at2，F=ma
得m=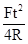
=4.5×10-3kg
最小动能的位置必在A点关于O点对称的B点, 则有F?2R=
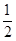mvA2-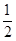mvB2 代入解得F=18N在A点时有 N-F=m
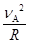
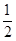mvA2=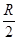（N-F）=18J所以最小动能为Ekm=
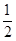mvB2=18J-14.4J=3.6J②在B点撤去轨道后，小球将做类平抛运动: 由2R=
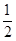at2，F=ma得m=
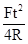=4.5×10-3kg
练习册系列答案
相关题目
，在A处放置一个质量为m的物体，现绕O点缓缓抬高A端，直到当木板转动到与水平面成α角的过程中，物体始终处于静止，在整个过程中（ ）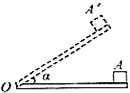
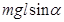
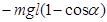
，其中k为劲度系数，x为弹簧的压缩量）
，且m>M．
物块的最终速度v。
