题目内容
一列简谐波某时刻的波形如图中实线所示.经过0.5s后的波形如图中的虚线所示.已知波的周期为T,且0.25s<T<0.5s,则( )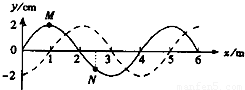
A.当波向+x方向传播时,波速等于10m/s
B.不论波向x轴哪一方向传播,在这0.5s内,x=1m处的质点M通过的路程都相等
C.当波沿+x方向传播时,x=1m处的质点M和x=2.5m处的质点N在这0.5s内通过的路程不相等
D.当波沿-x方向传播时,经过0.1s时,质点M的位移一定为零
【答案】分析:已知两个时刻的波形,波的传播方向可能沿向右,也可能向左.当波向右传播时,传播的最短距离是 波长,当波向左传播时,传播的最短距离是
波长,当波向左传播时,传播的最短距离是 波长,根据时间与周期的关系,求出周期,再求频率和波速及运动的位移和路程.
波长,根据时间与周期的关系,求出周期,再求频率和波速及运动的位移和路程.
解答:解:A、由图线可直接读出波长λ=4m.
因为0.25s<T<0.5s,
所以当波向+x方向传播时,0.5s=(0.25+n)T,当n=1时符合条件,解得T=0.4s,所以v=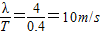 ,故A正确;
,故A正确;
C、在这0.5s内,x=1m处的质点M通过的路程sM=5A=10cm,x=2.5m处的质点N在前0.4s内通过的路程为4,后0.1s内向上运动,平均速度比从位移最大处运动的平均速度大,所以在后0.1s内的路程大于A,所以在这0.5s内通过的路程sN>5A,故C正确;
B、当波沿-x方向传播时,0.5s=(0.75+n)T,当n=1时符合条件,解得T= s,在这0.5s内,x=1m处的质点M通过的路程sM′=
s,在这0.5s内,x=1m处的质点M通过的路程sM′=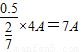 ,故B错误,
,故B错误,
D、当波沿-x方向传播时,T= s,而
s,而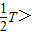 0.1s
0.1s ,质点M没有回到平衡位置,位移不为零,故D错误
,质点M没有回到平衡位置,位移不为零,故D错误
故选AC
点评:本题是利用波的时间周期性,求出周期,再求解波速的,也可以根据空间的周期性,求出波传播距离的通项,再求解波速,注意0.25s<T<0.5s,这个条件的应用.
 波长,当波向左传播时,传播的最短距离是
波长,当波向左传播时,传播的最短距离是 波长,根据时间与周期的关系,求出周期,再求频率和波速及运动的位移和路程.
波长,根据时间与周期的关系,求出周期,再求频率和波速及运动的位移和路程.解答:解:A、由图线可直接读出波长λ=4m.
因为0.25s<T<0.5s,
所以当波向+x方向传播时,0.5s=(0.25+n)T,当n=1时符合条件,解得T=0.4s,所以v=
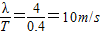 ,故A正确;
,故A正确;C、在这0.5s内,x=1m处的质点M通过的路程sM=5A=10cm,x=2.5m处的质点N在前0.4s内通过的路程为4,后0.1s内向上运动,平均速度比从位移最大处运动的平均速度大,所以在后0.1s内的路程大于A,所以在这0.5s内通过的路程sN>5A,故C正确;
B、当波沿-x方向传播时,0.5s=(0.75+n)T,当n=1时符合条件,解得T=
 s,在这0.5s内,x=1m处的质点M通过的路程sM′=
s,在这0.5s内,x=1m处的质点M通过的路程sM′=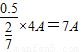 ,故B错误,
,故B错误,D、当波沿-x方向传播时,T=
 s,而
s,而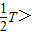 0.1s
0.1s ,质点M没有回到平衡位置,位移不为零,故D错误
,质点M没有回到平衡位置,位移不为零,故D错误故选AC
点评:本题是利用波的时间周期性,求出周期,再求解波速的,也可以根据空间的周期性,求出波传播距离的通项,再求解波速,注意0.25s<T<0.5s,这个条件的应用.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 (2009?武汉模拟)一列简谐波某时刻的波形如图中实线所示.经过0.5s后的波形如图中的虚线所示.已知波的周期为T,且0.25s<T<0.5s,则( )
(2009?武汉模拟)一列简谐波某时刻的波形如图中实线所示.经过0.5s后的波形如图中的虚线所示.已知波的周期为T,且0.25s<T<0.5s,则( ) (2007?湖南模拟)一列简谐波某时刻的波形图如图甲所示,乙图表示该波传播的介质中某质点此后一段时间内的振动图象.则( )
(2007?湖南模拟)一列简谐波某时刻的波形图如图甲所示,乙图表示该波传播的介质中某质点此后一段时间内的振动图象.则( ) 一列简谐波某时刻的波形如图所示,此波以0.5m/s的速度向左传播.这列波的周期T=
一列简谐波某时刻的波形如图所示,此波以0.5m/s的速度向左传播.这列波的周期T=
