题目内容
 (2009?武汉模拟)一列简谐波某时刻的波形如图中实线所示.经过0.5s后的波形如图中的虚线所示.已知波的周期为T,且0.25s<T<0.5s,则( )
(2009?武汉模拟)一列简谐波某时刻的波形如图中实线所示.经过0.5s后的波形如图中的虚线所示.已知波的周期为T,且0.25s<T<0.5s,则( )分析:已知两个时刻的波形,波的传播方向可能沿向右,也可能向左.当波向右传播时,传播的最短距离是
波长,当波向左传播时,传播的最短距离是
波长,根据时间与周期的关系,求出周期,再求频率和波速及运动的位移和路程.
| 1 |
| 4 |
| 3 |
| 4 |
解答:解:A、由图线可直接读出波长λ=4m.
因为0.25s<T<0.5s,
所以当波向+x方向传播时,0.5s=(0.25+n)T,当n=1时符合条件,解得T=0.4s,所以v=
=
=10m/s,故A正确;
C、在这0.5s内,x=1m处的质点M通过的路程sM=5A=10cm,x=2.5m处的质点N在前0.4s内通过的路程为4,后0.1s内向上运动,平均速度比从位移最大处运动的平均速度大,所以在后0.1s内的路程大于A,所以在这0.5s内通过的路程sN>5A,故C正确;
B、当波沿-x方向传播时,0.5s=(0.75+n)T,当n=1时符合条件,解得T=
s,在这0.5s内,x=1m处的质点M通过的路程sM′=
×4A=7A,故B错误,
D、当波沿-x方向传播时,T=
s,而
T>0.1s>
T,质点M没有回到平衡位置,位移不为零,故D错误
故选AC
因为0.25s<T<0.5s,
所以当波向+x方向传播时,0.5s=(0.25+n)T,当n=1时符合条件,解得T=0.4s,所以v=
| λ |
| T |
| 4 |
| 0.4 |
C、在这0.5s内,x=1m处的质点M通过的路程sM=5A=10cm,x=2.5m处的质点N在前0.4s内通过的路程为4,后0.1s内向上运动,平均速度比从位移最大处运动的平均速度大,所以在后0.1s内的路程大于A,所以在这0.5s内通过的路程sN>5A,故C正确;
B、当波沿-x方向传播时,0.5s=(0.75+n)T,当n=1时符合条件,解得T=
| 2 |
| 7 |
| 0.5 | ||
|
D、当波沿-x方向传播时,T=
| 2 |
| 7 |
| 1 |
| 2 |
| 1 |
| 4 |
故选AC
点评:本题是利用波的时间周期性,求出周期,再求解波速的,也可以根据空间的周期性,求出波传播距离的通项,再求解波速,注意0.25s<T<0.5s,这个条件的应用.

练习册系列答案
相关题目
 (2009?武汉模拟)如图,两个共轴的圆筒形金属电极,外电极接地,其上均匀分布着平行于轴线的四条狭缝a、b、c和d,外筒的外半径为r.在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场,磁感应强度的大小为B.在两极间加上电压,使两圆筒之间的区域内有沿半径向外的电场.一质量为m、带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零.如果该粒子经过一段时间的运动之后恰好又回到出发点S,则两电极之间的电压U应是多少?(不计重力,整个装置在真空中)
(2009?武汉模拟)如图,两个共轴的圆筒形金属电极,外电极接地,其上均匀分布着平行于轴线的四条狭缝a、b、c和d,外筒的外半径为r.在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场,磁感应强度的大小为B.在两极间加上电压,使两圆筒之间的区域内有沿半径向外的电场.一质量为m、带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零.如果该粒子经过一段时间的运动之后恰好又回到出发点S,则两电极之间的电压U应是多少?(不计重力,整个装置在真空中)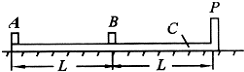 (2009?武汉模拟)如图所示,在水平桌面上放有长木板C,C上右端是固定挡板P,在C上左端和中点处各放有小物块A和B,A、B的尺寸以及P的厚度皆可忽略不计,A、B之间和B、P之间的距离皆为L.设木板C与桌面之间无摩擦,A、C之间和B、C之间的静摩擦因数及滑动摩擦因数均为μ;A、B、C(连同挡板P)的质量相同.开始时,B和C静止,A以某一初速度向右运动.试问下列情况是否能发生?要求定量求出能发生这些情况时物块A的初速度V0应满足的条件,或定量说明不能发生的理由.
(2009?武汉模拟)如图所示,在水平桌面上放有长木板C,C上右端是固定挡板P,在C上左端和中点处各放有小物块A和B,A、B的尺寸以及P的厚度皆可忽略不计,A、B之间和B、P之间的距离皆为L.设木板C与桌面之间无摩擦,A、C之间和B、C之间的静摩擦因数及滑动摩擦因数均为μ;A、B、C(连同挡板P)的质量相同.开始时,B和C静止,A以某一初速度向右运动.试问下列情况是否能发生?要求定量求出能发生这些情况时物块A的初速度V0应满足的条件,或定量说明不能发生的理由.