Question

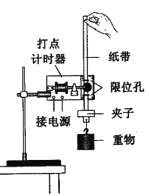
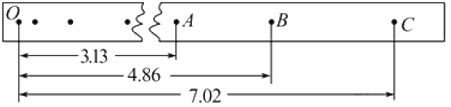
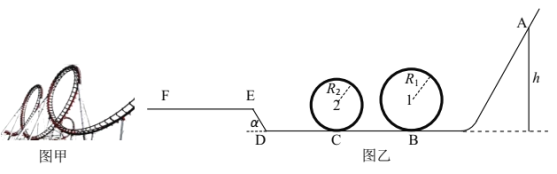
【题目】图甲是某游乐场的一种“双环过山车”设施的一部分，其运行原理可以简化成图乙的“小球轨道”模型。其中AB段和圆轨道不计阻力，BC、CD、DE、EF段平直轨道与小球的动摩擦因数为μ=0.2，DE段的倾角α=53°，B、C为两竖直圆轨道1、2的最低点，LBC=LCD=6m，LDE=1m，LEF=10m，半径R1=2m。质量为m=1kg的小球（视为质点），从轨道的右侧A点由静止开始下滑，设小球不脱离所有轨道，且不考虑D、E点的能量损失，（已知cos37°=0.8，重力加速度取g=10m/s2）试求：

（1）如果小球恰能通过第一个圆轨道，A点的高度h应是多少；

（2）要使小球不脱离第二个圆轨道，半径R2应满足的条件；

（3）要使小球最终停在EF段，A点的高度h应该设计为多少。

Answer 1

【答案】（1）5m；（2）R2≤1.52m或R2≥3.8m；（3）5m≤h≤5.32m

【解析】

（1）小球恰好能过竖直圆轨道，则在最高点满足

小球从A点到最高点根据机械能守恒定律有

联立解得h=5m

（2）要保证小球不脱离轨道，可分两种情况进行讨论：

I.轨道半径较小时，小球恰能通过第二个圆轨道，设在最高点的速度为v2，应满足

同时满足，小球能通过第一轨道，根据动能定理有

或者

联立解得R2=1.52m

II.轨道半径较大时，小球上升的最大高度为R2，根据动能定理

或者

联立解得R2=3.8m

故R2≤1.52m或R2≥3.8m

（3）如果小球停止在E点，从出发到E点，根据动能定理得

解得h=3.32m<5m

说明小球刚好到E点就过不了竖直圆轨道，如果小球停止在F点，从出发到F点根据动能定理得:

解得h=5.32m

综上可得5m≤h≤5.32m