题目内容
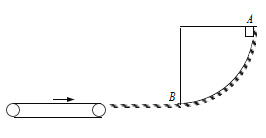
【题目】如图所示，四分之一的光滑圆弧轨道AB 与水平轨道平滑相连，圆弧轨道的半径为R=0.8m，有一质量为m=1kg 的滑块从A端由静止开始下滑，滑块与水平轨道间的动摩擦因数为μ=0.5，滑块在水平轨道上滑行L=0.7m 后，滑上一水平粗糙的传送带，传送带足够长且沿顺时针方向转动，取 g=10m/s2，求：
（1）滑块第一次滑上传送带时的速度 v1 多大？
（2）若要滑块再次经过B点，传送带的速度至少多大？
（3）试讨论传送带的速度v与滑块最终停下位置x（到B点的距离）的关系。
【答案】(1) 3m/s (2) 
m/s (3) 
或
【解析】
（1）从A点到刚滑上传送带，应用动能定理
得
代入数据得，v1=3m/s.
（2）滑块在传送带上运动，先向左减速零，再向右加速，若传送带的速度小于v1，则物块最终以传送带的速度运动，设传送带速度为v时，物块刚能滑到B点，则
解得
m/s
即传送带的速度必须大于等于m/s。
(3)传送带的速度大于或等于v1，则滑块回到水平轨道时的速度大小仍为v1
得s=0.9m，即滑块在水平轨道上滑行的路程为0.9m，则最后停在离B点0.2m处。
若传送带的速度m/s <v<3m/s，则滑块将回到B点，滑上圆弧轨道后又滑到水平轨道，最后停下，即
解得
若传送带的速度v<m/s，则滑块将不能回到B点，即
解得
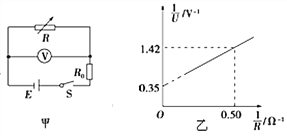
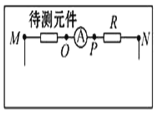
【题目】某实验小组的同学在学校实验室中发现一电学元件,该电学元件上标有“最大电流不超过6mA,最大电压不超过7V”,同学们想通过实验描绘出该电学元件的伏安特性曲线,他们设计的一部分电路如图所示,图中定值电阻R=1kΩ,用于限流;电流表量程为10mA,内阻约为5Ω;电压表（未画出）量程为10V，内阻约为10kΩ；电源电动势E为12V，内阻不计。
（1）实验时有两个滑动变阻器可供选择：
A．阻值0～200Ω，额定电流0.3A
B．阻值0～20Ω，额定电流1A
应选的滑动变阻器是___（选填“A”或“B”）。
正确连线后，测得数据如表：
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
U/V | 0.00 | 3.00 | 6.00 | 6.16 | 6.28 | 6.32 | 6.36 | 6.38 | 6.39 | 6.40 |
I/mA | 0.00 | 0.00 | 0.00 | 0.06 | 0.50 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 |
（2）由以上数据分析可知,电压表应并联在M与_______（选填“O”或“P”）之间。
（3）在图中将电路图补充完整。
（______）
（4）从表中数据可知，该电学元件的电阻特点是：_______________。
