题目内容
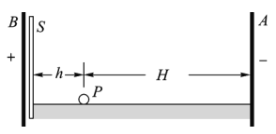
【题目】如图，竖直固定挡板与静置于水平轨道上的小物块a之间夹有压缩的轻质弹簧，弹簧被锁定且与a接触但不粘连。水平轨道的MN段粗糙，其余部分光滑。N处有一小物块b，用不可伸长轻质细绳悬挂于某点O处。某时刻弹簧解锁，弹簧恢复原长后，a进入MN段，之后与b发生碰撞并粘连在一起。已知a与MN段的动摩擦因数为0.5，MN长度为l， a、b质量均为m，重力加速度为g。弹簧被锁定时的弹性势能为1.5mgl，细绳能承受的拉力最大值为20mg。
（1）求a与b碰前瞬间a的速率；
（2）a、b碰后，若要细绳始终拉直，求细绳的长度r需满足的条件。
【答案】（1）
；（2）
或
【解析】
（1）对小物块，从释放到N点，由动能定理可得
解得
（2）a、b碰撞过程由动量守恒得
碰撞后两物体做圆周运动，故
由
解得，
若物体能到最高点，则在最高点
从最低点到最高点
解得
若物体最多运动到与圆心等高的位置
解得
综上所述细绳的长度r需满足的条件为
或
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
