题目内容
5. 如图,实心金属球A半径为R,带电量为Q,点电荷B带电量为q.B与A球间的距离为r.当B不存在而只有A存在且达到静电平衡状态时,电荷Q在球心O处的电场强度等于0.当点电荷B也同时存在并达到静电平衡时,球心O处的电场强度等于0,金属球上的电荷在球心O处产生的场强的大小等于$\frac{kq}{{r}^{2}}$.
如图,实心金属球A半径为R,带电量为Q,点电荷B带电量为q.B与A球间的距离为r.当B不存在而只有A存在且达到静电平衡状态时,电荷Q在球心O处的电场强度等于0.当点电荷B也同时存在并达到静电平衡时,球心O处的电场强度等于0,金属球上的电荷在球心O处产生的场强的大小等于$\frac{kq}{{r}^{2}}$.
分析 静电感应的过程,是导体A(含大地)中自由电荷在电荷Q所形成的外电场下重新分布的过程,当处于静电平衡状态时,在导体内部电荷Q所形成的外电场E与感应电荷产生的“附加电场E′”同时存在的,且在导体内部任何一点,外电场电场场强E与附加电场的场强E'大小相等,方向相反.
解答 解:根据静电平衡状态的特点可知,孤立导体内部的电场强度为0.所以当B不存在而只有A存在且达到静电平衡状态时,电荷Q在球心O处的电场强度是0;
球外点电荷在O点产生的场强,据点电荷的场强公式得:E=$\frac{kq}{{r}^{2}}$
利用静电平衡的特点,内部场强处处为零,即感应电荷在导体内部产生的电场与球外电荷产生的电场强度大小相等,
所以E′=E=$\frac{kq}{{r}^{2}}$
故答案为:0,0,$\frac{kq}{{r}^{2}}$
点评 明确静电平衡导体的特点,即内部场强处处为零,是个等势体,注意合场强与各个电荷产生场强的关系.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
15.关于多用电表面板上的刻度线,下列说法中正确的是( )
| A. | 直流电流刻度线和直流电压刻度线都是均匀的,可共用同一刻度线 | |
| B. | 电阻刻度线是均匀的,且每一档的测量范围都是从0~∞ | |
| C. | 交流电压刻度线是均匀的 | |
| D. | 电阻刻度线上的零欧姆刻度线与直流电流刻度的最大刻度线相对应 |
16. 一绝缘细线oa下端系一质量为m的带正电小球a,在正下方有一光滑的绝缘水平细杆,一带负电的小球b穿过杆处在左侧较远处,小球a由于受到水平绝缘细线的拉力而静止,如图所示.现保持悬线与竖直方的向夹角为θ,从静止开始在较远处释放小球b,让其从远处沿杆向右移动到a点的正下方,在此过程中下列说法错误的是( )
一绝缘细线oa下端系一质量为m的带正电小球a,在正下方有一光滑的绝缘水平细杆,一带负电的小球b穿过杆处在左侧较远处,小球a由于受到水平绝缘细线的拉力而静止,如图所示.现保持悬线与竖直方的向夹角为θ,从静止开始在较远处释放小球b,让其从远处沿杆向右移动到a点的正下方,在此过程中下列说法错误的是( )
 一绝缘细线oa下端系一质量为m的带正电小球a,在正下方有一光滑的绝缘水平细杆,一带负电的小球b穿过杆处在左侧较远处,小球a由于受到水平绝缘细线的拉力而静止,如图所示.现保持悬线与竖直方的向夹角为θ,从静止开始在较远处释放小球b,让其从远处沿杆向右移动到a点的正下方,在此过程中下列说法错误的是( )
一绝缘细线oa下端系一质量为m的带正电小球a,在正下方有一光滑的绝缘水平细杆,一带负电的小球b穿过杆处在左侧较远处,小球a由于受到水平绝缘细线的拉力而静止,如图所示.现保持悬线与竖直方的向夹角为θ,从静止开始在较远处释放小球b,让其从远处沿杆向右移动到a点的正下方,在此过程中下列说法错误的是( )| A. | 悬线oa的拉力逐渐增大 | B. | 水平细线的拉力在逐渐减小 | ||
| C. | b球的速度始终增大 | D. | b球的加速度为先增大后减小 |
13.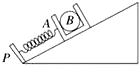 如图所示,置于足够长斜面上的盒子A内放有光滑球B,B恰与盒子前、后壁接触,斜面光滑且放置于粗糙水平地面上.一轻质弹簧的一端与固定在斜面上的木板P拴接,另一端与A相连.今用外力推A使弹簧处于压缩状态,然后由静止释放盒子,释放盒子前后斜面始终相对地面处于静止状态,下列说法不正确的是( )
如图所示,置于足够长斜面上的盒子A内放有光滑球B,B恰与盒子前、后壁接触,斜面光滑且放置于粗糙水平地面上.一轻质弹簧的一端与固定在斜面上的木板P拴接,另一端与A相连.今用外力推A使弹簧处于压缩状态,然后由静止释放盒子,释放盒子前后斜面始终相对地面处于静止状态,下列说法不正确的是( )
 如图所示,置于足够长斜面上的盒子A内放有光滑球B,B恰与盒子前、后壁接触,斜面光滑且放置于粗糙水平地面上.一轻质弹簧的一端与固定在斜面上的木板P拴接,另一端与A相连.今用外力推A使弹簧处于压缩状态,然后由静止释放盒子,释放盒子前后斜面始终相对地面处于静止状态,下列说法不正确的是( )
如图所示,置于足够长斜面上的盒子A内放有光滑球B,B恰与盒子前、后壁接触,斜面光滑且放置于粗糙水平地面上.一轻质弹簧的一端与固定在斜面上的木板P拴接,另一端与A相连.今用外力推A使弹簧处于压缩状态,然后由静止释放盒子,释放盒子前后斜面始终相对地面处于静止状态,下列说法不正确的是( )| A. | 弹簧恢复原长时AB速度最大 | |
| B. | 弹簧恢复原长时B对A的作用力为零 | |
| C. | AB沿斜面向上运动的过程中地面对斜面的支持力不断变小 | |
| D. | AB沿斜面向上运动的过程中地面对斜面的摩擦力始终向左 |
10.如图为一块手机电池的背面印有的一些符号,下列说法正确的是( )


| A. | 该电池的容量为 500 mA•h | |
| B. | 该电池的电动势为3.6 V | |
| C. | 该电池在工作1 小时后达到的电流为 500 mA | |
| D. | 若电池以 10 mA的电流工作,可用 50 小时 |
15.一小木块以初速度5m/s自由冲上光滑的斜面,2s末速度大小变为1m/s,则这段时间内小木块的加速度大小( )
| A. | 一定为2 m/s2 | B. | 一定为3 m/s2 | C. | 可能大于2m/s2 | D. | 可能小于2 m/s2 |
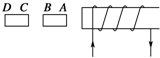 如图所示,两块软铁放在螺线管轴线上,当螺线管通电后,两软铁将吸引(填“吸引”“排斥”或“无作用力”),A端将磁化为S极.
如图所示,两块软铁放在螺线管轴线上,当螺线管通电后,两软铁将吸引(填“吸引”“排斥”或“无作用力”),A端将磁化为S极. 如图是某种静电分选器的原理示意图,两个竖直放置的平行金属板带有等量异号电荷,形成匀强电场.分选器漏斗的出口与两板上端处于同一高度,到两板距离相等.混合在一起的a、b两种颗粒从漏斗出口下落时,a种颗粒带上正电,b种颗粒带上负电.经分选电场后,a、b两种颗粒分别落到水平传送带A、B上.已知两板间距d=0.1m,板的长度l=0.5m,电场仅局限在平行板之间;各颗粒所带电量大小与其质量之比均为1×10-5C/kg.设颗粒进入电场时的初速度为零,分选过程中颗粒大小及颗粒间的相互作用力不计.要求两种颗粒离开电场区域时,不接触到极板但有最大偏转量.重力加速度g取10m/s2.求:
如图是某种静电分选器的原理示意图,两个竖直放置的平行金属板带有等量异号电荷,形成匀强电场.分选器漏斗的出口与两板上端处于同一高度,到两板距离相等.混合在一起的a、b两种颗粒从漏斗出口下落时,a种颗粒带上正电,b种颗粒带上负电.经分选电场后,a、b两种颗粒分别落到水平传送带A、B上.已知两板间距d=0.1m,板的长度l=0.5m,电场仅局限在平行板之间;各颗粒所带电量大小与其质量之比均为1×10-5C/kg.设颗粒进入电场时的初速度为零,分选过程中颗粒大小及颗粒间的相互作用力不计.要求两种颗粒离开电场区域时,不接触到极板但有最大偏转量.重力加速度g取10m/s2.求: