Question

【题目】一根弹性细绳劲度系数为k，将其一端固定，另一端穿过一光滑小孔O系住一质量为m的滑块，滑块放在水平地面上。当细绳竖直时，小孔O到悬点的距离恰为弹性细绳原长，小孔O到正下方水平地面上 P点的距离为h（h），滑块与水平地面间的动摩擦因数为，设最大静摩擦力等于滑动摩擦力，弹性细绳始终在其弹性限度内，求：

(1)当滑块置于水平面能保持静止时，滑块到P点的最远距离；

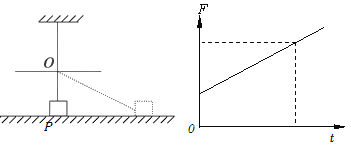
(2)如果滑块从P点向右匀速运动，就需给滑块一水平向右的力F，力F与时间t的关系为如图所示的直线，已知图线的斜率为b，根据图线求滑块匀速运动的速度；

(3)若在上述匀速运动的过程中，滑块从P点向右运动了S的距离，求拉力F所做的功。

Answer 1

【答案】(1)；(2)；(3)

【解析】

(1)设滑块离P点最远时，弹性绳伸长x，弹性绳与水平面夹角为θ，滑块到P点的最远距离为L，受力如图所示，

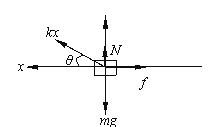
kxcosθ=μN…①

N+kxsinθ=mg…②

又h=xsinθ…③

L=xcosθ…④

由①②③④解得：

(2)滑块向右匀速运动时，受力如图所示

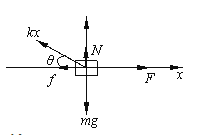
F=kxcosθ+μN…⑤

N+kxsinθ=mg…⑥

又vt=xcosθ…⑦

由③⑤⑥⑦解得：F=kvt+μ（mg-kh）

结合F与时间t的关系图线，可得：kv=b，故

(3)设滑块匀速移动的位移为S，有：

s=vt…⑧

由⑤⑥⑧得：F=ks+μ（mg-kh）

由此作出F-S的关系图线如图

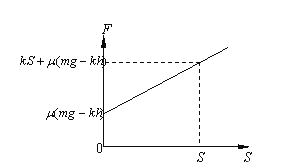
则图线所围成的面积即为外力F所做的功：